题目内容
已知函数 ,
,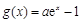 (其中
(其中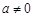 ,
,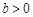 ),且函数
),且函数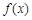 的图象在 点
的图象在 点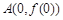 处的切线与函数
处的切线与函数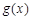 的图象在点
的图象在点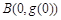 处的切线重合.
处的切线重合.
(Ⅰ)求实数a,b的值;
(Ⅱ)若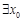 ,满足
,满足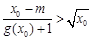 ,求实数m的取值范围;
,求实数m的取值范围;
(1)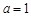 ,
,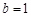 (2)
(2)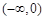
解析试题分析:解:(Ⅰ)∵ ,∴
,∴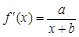 ,
,
则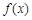 在点
在点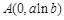 处切线的斜率
处切线的斜率 ,切点
,切点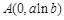 ,
,
则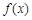 在点
在点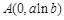 处切线方程为
处切线方程为 , 2分
, 2分
又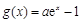 ,∴
,∴ ,
,
则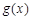 在点
在点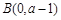 处切线的斜率
处切线的斜率 ,切点
,切点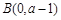 ,
,
则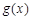 在点
在点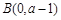 处切线方程为
处切线方程为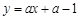 , 4分
, 4分
由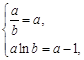 解得
解得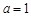 ,
,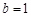 . 6分
. 6分
(Ⅱ)由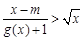 得
得 ,故
,故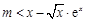 在
在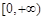 上有解,
上有解,
令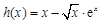 ,只需
,只需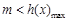 . 8分
. 8分
①当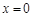 时,
时, ,所以
,所以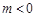 ; 10分
; 10分
②当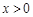 时,∵
时,∵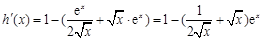 ,
,
∵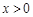 ,∴
,∴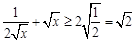 ,
,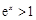 ,∴
,∴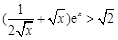 ,
,
故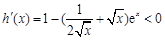 ,即函数
,即函数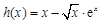 在区间
在区间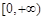 上单调递减,
上单调递减,
所以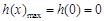 ,此时
,此时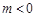 . 13分
. 13分
综合①②得实数m的取值范围是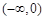 . 14分
. 14分
考点:导数的运用
点评:解决的关键是对于导数的符号与函数单调性的关系的运用,属于基础题。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 在区间
在区间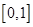 上是增函数,在区间
上是增函数,在区间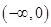 ,
,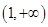 上是减函数,又
上是减函数,又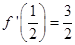
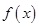 的解析式;
的解析式;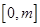
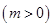 上恒有
上恒有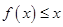 成立,求
成立,求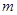 的取值范围
的取值范围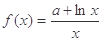 ,且
,且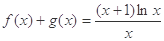 。
。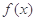 在
在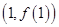 处的切线与
处的切线与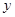 轴垂直,求
轴垂直,求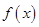 的极值。
的极值。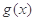 在
在 ,求实数a的值。
,求实数a的值。 。(Ⅰ)若函数
。(Ⅰ)若函数 在
在 处与直线
处与直线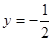 相切,①求实数
相切,①求实数 ,b的值;②求函数
,b的值;②求函数 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当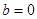 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数m的取值范围。
都成立,求实数m的取值范围。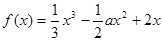 ,讨论
,讨论 的单调性.
的单调性. .
. 的单调区间与极值;
的单调区间与极值; ,使得对任意的
,使得对任意的 ,当
,当 时恒有
时恒有 成立.若存在,求
成立.若存在,求 ,其中
,其中 .
. 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求 的取值范围;
的取值范围; ,如果存在
,如果存在 ,使得函数
,使得函数
 在
在 处取得最小值,试求
处取得最小值,试求 的最大值.
的最大值.  其中
其中 ,曲线
,曲线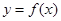 在点
在点 处的切线垂直于
处的切线垂直于 轴.
轴. 的值;
的值; 的极值.
的极值.