题目内容
甲、乙、丙三人参加了一家公司的招聘面试,设每人面试合格的概率都是 ,且面试是否合格互不影响求:
,且面试是否合格互不影响求:
(1)三人面试都不合格的概率;
(2)至少有1人面试合格的概率.
解:(1)设“甲、乙、丙三人每个人面试合格”分别为事件A,B,C,则P(A)=P(B)=P(C)= ,
,
则三人面试都不合格的概率为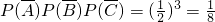 .
.
(2)至少有1人面试合格的概率是1减去每个人面试都不合格的概率,
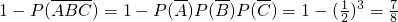 .
.
分析:(1)设“甲、乙、丙三人每个人面试合格”分别为事件A,B,C,则三人面试都不合格的概率为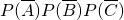 ,运算求得结果.
,运算求得结果.
(2)根据“至少有1人面试合格的概率”是 1减去每个人面试都不合格的概率,可得所求的概率为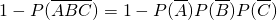 ,运算求得结果.
,运算求得结果.
点评:本题考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,所求的事件与它的对立事件概率间的关系,利用
所求的事件与它的对立事件概率间的关系,是解题的关键.
 ,
,则三人面试都不合格的概率为
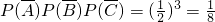 .
.(2)至少有1人面试合格的概率是1减去每个人面试都不合格的概率,
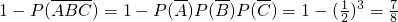 .
.分析:(1)设“甲、乙、丙三人每个人面试合格”分别为事件A,B,C,则三人面试都不合格的概率为
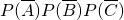 ,运算求得结果.
,运算求得结果.(2)根据“至少有1人面试合格的概率”是 1减去每个人面试都不合格的概率,可得所求的概率为
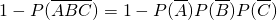 ,运算求得结果.
,运算求得结果.点评:本题考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,所求的事件与它的对立事件概率间的关系,利用
所求的事件与它的对立事件概率间的关系,是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目