题目内容
(2011•东城区一模)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为
,乙、丙面试合格的概率都是
,且面试是否合格互不影响.
(Ⅰ)求至少有1人面试合格的概率;
(Ⅱ)求签约人数ξ的分布列和数学期望.
| 1 |
| 2 |
| 1 |
| 3 |
(Ⅰ)求至少有1人面试合格的概率;
(Ⅱ)求签约人数ξ的分布列和数学期望.
分析:(Ⅰ)用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,且P(A)=
,P(B)=P(C)=
.由至少有1人面试合格的概率是1-P(
),能求出至少有1人面试合格的概率.(Ⅱ)ξ的可能取值为0,1,2,3.分别求了P(ξ=0),P(ξ=1),P(ξ=2)和P(ξ=3),由此能求出ξ的分布列和ξ的期望Eξ.
| 1 |
| 2 |
| 1 |
| 3 |
. |
| A |
. |
| B |
. |
| C |
解答:解:(Ⅰ)用A,B,C分别表示事件甲、乙、丙面试合格.
由题意知A,B,C相互独立,
且P(A)=
,P(B)=P(C)=
.
至少有1人面试合格的概率是:
1-P(
)
=1-P(
) P(
) P(
)
=1-
×
×
=
.
(Ⅱ)ξ的可能取值为0,1,2,3.
P(ξ=0)=P(
B
)+P(
C)+P(
)
=P(
)P(B)P(
)+P(
) P(
) P(C)+P(
)P(
) P(
)
=
×
×
+
×
×
+
×
×
=
.
P(ξ=1)=P(A
C)+P(AB
)+P(A
)
=P(A)P(
) P(C)+P(A)P(B)P(
)P(A)P(
) P(
)
=
×
×
+
×
×
+
×
×
=
,
P(ξ=2)=P(
BC)=
×
×
=
,
P(ξ=3)=P(ABC)=P(A)P(B)P(C)=
×
×
=
.
∴ξ的分布列是
故ξ的期望Eξ=0×
+1×
+2×
+3×
=
.
由题意知A,B,C相互独立,
且P(A)=
| 1 |
| 2 |
| 1 |
| 3 |
至少有1人面试合格的概率是:
1-P(
. |
| A |
. |
| B |
. |
| C |
=1-P(
. |
| A |
. |
| B |
. |
| C |
=1-
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
=
| 7 |
| 9 |
(Ⅱ)ξ的可能取值为0,1,2,3.
P(ξ=0)=P(
. |
| A |
. |
| C |
. |
| A |
. |
| B |
. |
| A |
. |
| B |
. |
| C |
=P(
. |
| A |
. |
| C |
. |
| A |
. |
| B |
. |
| A |
. |
| B |
. |
| C |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
=
| 4 |
| 9 |
P(ξ=1)=P(A
. |
| B |
. |
| C |
. |
| B |
. |
| C |
=P(A)P(
. |
| B |
. |
| C |
. |
| B |
. |
| C |
=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
P(ξ=2)=P(
. |
| A |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 18 |
P(ξ=3)=P(ABC)=P(A)P(B)P(C)=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 18 |
∴ξ的分布列是
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P(ξ) |
|
|
|
|
| 4 |
| 9 |
| 4 |
| 9 |
| 1 |
| 18 |
| 1 |
| 18 |
| 13 |
| 18 |
点评:本题考查离散型随机变量的分布列和数学期望,考查学生的运算能力,考查学生探究研究问题的能力,解题时要认真审题,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
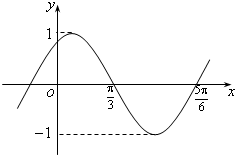 (2011•东城区一模)已知函数y=sin(ωx+φ)
(2011•东城区一模)已知函数y=sin(ωx+φ)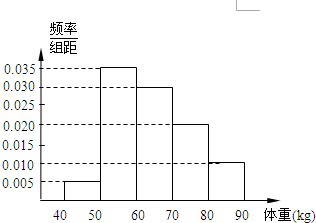 (2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为
(2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为