题目内容
(1)已知函数f(2x)=x2+x,求函数f(x)和f(x+1)的解析式.
(2)讨论函数f(x)=x+
在[2,+∞)上的单调性.
(2)讨论函数f(x)=x+
| 4 |
| x |
(1)令:2x=t,
则有x=
t,
∴f(t)=
t2+
t
∴f(x)=
x2+
x
f(x+1)=
(x+1)2+
(x+1)=
x2+x+
;
(2)由于x∈[2,+∞),则f′(x)=1-
≥0恒成立
故函数f(x)=x+
在[2,+∞)上的单调递增.
则有x=
| 1 |
| 2 |
∴f(t)=
| 1 |
| 4 |
| 1 |
| 2 |
∴f(x)=
| 1 |
| 4 |
| 1 |
| 2 |
f(x+1)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
(2)由于x∈[2,+∞),则f′(x)=1-
| 4 |
| x2 |
故函数f(x)=x+
| 4 |
| x |

练习册系列答案
相关题目
 上的函数
上的函数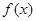 满足
满足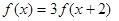 .当
.当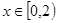 时
时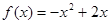 .设
.设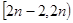 上的最大值为
上的最大值为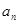 ,且数列
,且数列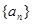 的前
的前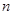 项和为
项和为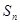 ,则
,则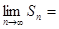 . (其中
. (其中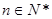 )
)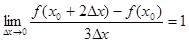 ,则
,则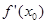 等于 ( )
等于 ( )
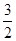
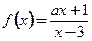 的反函数就是
的反函数就是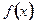 本身,则
本身,则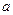 的值为
的值为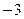
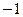
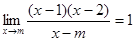 ,则实数
,则实数 的值为
的值为