题目内容
对于每个实数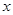 ,设
,设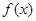 取
取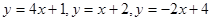 三个函数中的最小值, 则
三个函数中的最小值, 则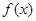 的最大值为
的最大值为
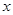 ,设
,设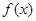 取
取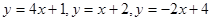 三个函数中的最小值, 则
三个函数中的最小值, 则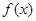 的最大值为
的最大值为A.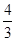 | B.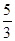 | C.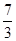 | D.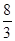 |
D
函数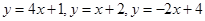 的图象如下:
的图象如下:
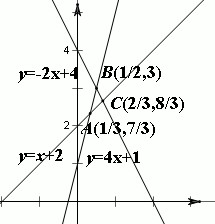
由图可知,当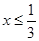 时,
时, ;当
;当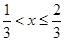 时,
时,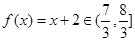 ;当
;当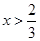 时,
时,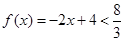 。综上可得,
。综上可得,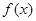 的最大值为
的最大值为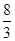 ,故选D
,故选D
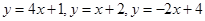 的图象如下:
的图象如下:
由图可知,当
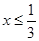 时,
时, ;当
;当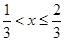 时,
时,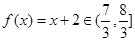 ;当
;当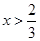 时,
时,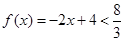 。综上可得,
。综上可得,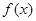 的最大值为
的最大值为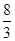 ,故选D
,故选D
练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
题目内容
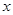 ,设
,设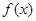 取
取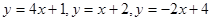 三个函数中的最小值, 则
三个函数中的最小值, 则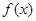 的最大值为
的最大值为A.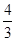 | B.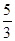 | C.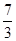 | D.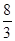 |
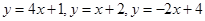 的图象如下:
的图象如下:
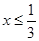 时,
时, ;当
;当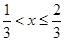 时,
时,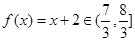 ;当
;当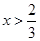 时,
时,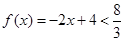 。综上可得,
。综上可得,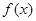 的最大值为
的最大值为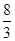 ,故选D
,故选D
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案