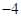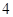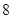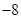题目内容
偶函数 在
在 上为增函数,若不等式
上为增函数,若不等式 对
对 恒成立,则实数a的取值范围为
恒成立,则实数a的取值范围为
A. | B. | C. | D. |
B
解析试题分析:根据偶函数图象关于原点对称,得f(x)在[0,+∞)上单调增且在(-∞,0]上是单调减函,由此结合2+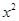 是正数,将原不等式转化为|ax-1|<2+x2恒成立,去绝对值再用一元二次不等式恒成立的方法进行处理,即得实数a的取值范围.解:∵f(x)是偶函数,图象关于y轴对称,∴f(x)在[0,+∞)上的单调性与的单调性相反,由此可得f(x)在(-∞,0]上是减函数,∴不等式f(ax-1)<f(2+
是正数,将原不等式转化为|ax-1|<2+x2恒成立,去绝对值再用一元二次不等式恒成立的方法进行处理,即得实数a的取值范围.解:∵f(x)是偶函数,图象关于y轴对称,∴f(x)在[0,+∞)上的单调性与的单调性相反,由此可得f(x)在(-∞,0]上是减函数,∴不等式f(ax-1)<f(2+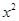 )恒成立,等价于|ax-1|<2+x2恒成立,即不等式-2-
)恒成立,等价于|ax-1|<2+x2恒成立,即不等式-2-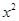 <ax-1<2+
<ax-1<2+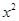 恒成立,得
恒成立,得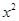 +ax+1>0
+ax+1>0
, x2-ax+3>0的解集为R,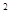 ∴结合一元二次方程根的判别式,得:
∴结合一元二次方程根的判别式,得: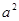 -4<0且(-a)2-12<0,解之得-2<a<2,故选:B
-4<0且(-a)2-12<0,解之得-2<a<2,故选:B
考点:偶函数的单调性
点评:本题给出偶函数的单调性,叫我们讨论关于x的不等式恒成立的问题,着重考查了函数的单调性与奇偶性、一元二次不等式解法等知识,属于基础题

练习册系列答案
相关题目
若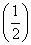 2a+1<
2a+1<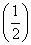 3-2a,则实数a的取值范围是( ).
3-2a,则实数a的取值范围是( ).
| A.(1,+∞) | B.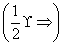 |
| C.(-∞,1) | D.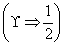 |
已知函数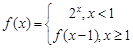 ,则
,则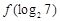 =( )
=( )
A.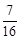 | B.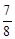 | C.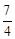 | D.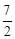 |
定义在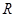 上的奇函数
上的奇函数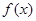 满足
满足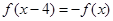 ,且在
,且在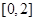 上单调递增,则
上单调递增,则
A.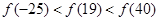 | B.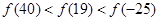 |
C.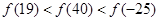 | D.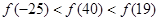 |
设函数 的图象上的点
的图象上的点 处的切线的斜率为
处的切线的斜率为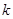 ,记
,记 ,则函数
,则函数 的图象大致为( )
的图象大致为( )
| A. | B. | C. | D. |
已知函数
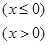 ,使函数值为5的
,使函数值为5的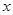 的值是( )
的值是( )
| A.-2 | B.2或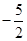 | C.2或-2 | D.2或-2或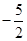 |
已知f(x)是定义在(0,+ )上的非负可导函数,且满足
)上的非负可导函数,且满足 。对任意正数a、b,若a<b,则必有( )
。对任意正数a、b,若a<b,则必有( )
| A.af(b)≤bf(a) | B.bf(a)≤af(b) |
| C.af(a)≤f(b) | D. bf(b)≤f(a) |
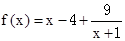 ,
,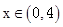 ,当
,当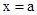 时,
时,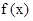 取得最小值
取得最小值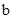 ,则函数
,则函数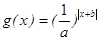 的图象为( )
的图象为( )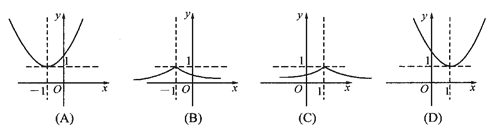
 ”表示一种运算,即:
”表示一种运算,即: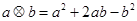 ,设函数
,设函数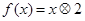 。且关于
。且关于 的方程为
的方程为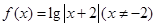 恰有四个互不相等的实数根
恰有四个互不相等的实数根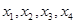 ,则
,则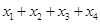 的值是( )
的值是( )