题目内容
规定记号“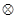 ”表示一种运算,即:
”表示一种运算,即: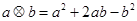 ,设函数
,设函数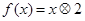 。且关于
。且关于 的方程为
的方程为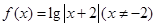 恰有四个互不相等的实数根
恰有四个互不相等的实数根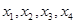 ,则
,则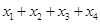 的值是( )
的值是( )
A.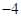 | B.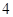 | C.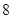 | D.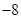 |
D.
解析试题分析:因为规定记号“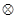 ”表示一种运算,即:
”表示一种运算,即: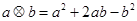 ,所以
,所以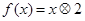 =
=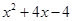 ,方程为
,方程为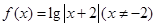 恰有四个互不相等的实数根
恰有四个互不相等的实数根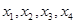 ,即
,即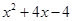 =
=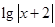 恰有四个互不相等的实数根
恰有四个互不相等的实数根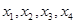 ,因为f(x),g(x)=
,因为f(x),g(x)=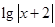 的图象均关于直线x=-2对称,即若-2+x是方程的根,则-2-x也是方程的根,所以
的图象均关于直线x=-2对称,即若-2+x是方程的根,则-2-x也是方程的根,所以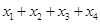 的值是-8,选D。
的值是-8,选D。
考点:本题主要考查函数图象的对称性,对数函数、二次函数图象和性质。
点评:新定义问题,实质是对函数图象的对称性、对数函数、二次函数图象和性质的考查,因为图象关于直线x=-2对称,所以有若-2+x是方程的根,则-2-x也是方程的根。

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
已知函数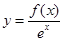 ,满足
,满足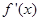 >
> ,则
,则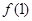 与
与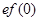 的大小关系是( )
的大小关系是( )
A.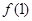 < <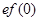 | B.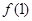 > >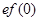 |
C.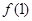 = = 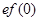 | D.不能确定 |
函数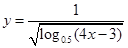 的定义域为( )
的定义域为( )
A.(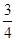 ,1) ,1) | B.(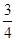 ,+∞) ,+∞) | C.(1,+∞) | D.(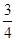 ,1)∪(1,+∞) ,1)∪(1,+∞) |
已知函数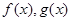 是定义在R上可导函数,满足
是定义在R上可导函数,满足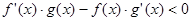 ,且
,且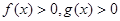 ,对
,对 时。下列式子正确的是( )
时。下列式子正确的是( )
A. | B.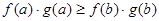 |
C.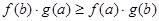 | D.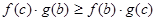 |
偶函数 在
在 上为增函数,若不等式
上为增函数,若不等式 对
对 恒成立,则实数a的取值范围为
恒成立,则实数a的取值范围为
A. | B. | C. | D. |
给右图的容器甲注水,下面图像中哪一个图像可以大致刻画容器中水的高度与时间的函数关系:( )。
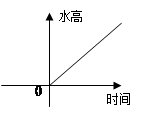
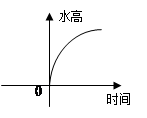
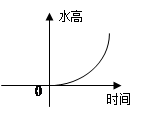

| A. | B. | C. | D. |
下列函数中是偶函数的是( )
A.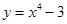 | B.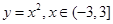 |
C.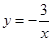 | D.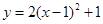 |
设函数 ,
, . 若当
. 若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( ).
的取值范围是( ).
A. | B. | C. | D. |
函数 的单调递增区间( )
的单调递增区间( )
A. | B.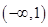 | C. | D. |