题目内容

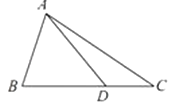
【题目】要测量电视塔AB的高度，在C点测得塔顶的仰角是45°，在D点测得塔顶的仰角是30°，并测得水平面上的∠BCD=120°，CD=40m，则电视塔的高度是（ ）
A.30m
B.40m
C. m
D. m

【答案】B
【解析】解：由题题意，设AB=x，则BD= x，BC=x 在△DBC中，∠BCD=120°，CD=40，
∴根据余弦定理，得BD2=BC2+CD2﹣2BCCDcos∠DCB
即：（ x）2=（40）2+x2﹣2×40xcos120°
整理得x2﹣20x﹣800=0，解之得x=40或x=﹣20（舍）
即所求电视塔的高度为40米．
故选B．

设出AB=x，进而根据题意将BD、DC用x来表示，然后在△DBC中利用余弦定理建立方程求得x，即可得到电视塔的高度．

练习册系列答案
相关题目

【题目】如图，在△ABC中，AB=2， cos2B+5cosB﹣ =0，且点D在线段BC上．
（1）若∠ADC= ，求AD的长；
（2）若BD=2DC， =4 ，求△ABD的面积．

【题目】已知函数f（x）=lnx﹣ax+ ，且f（x）+f（ ）=0，其中a，b为常数．
（1）若函数f（x）的图象在x=1的切线经过点（2，5），求函数的解析式；
（2）已知0＜a＜1，求证：f（ ）＞0；
（3）当f（x）存在三个不同的零点时，求a的取值范围．

【题目】设函数f（x）=|x﹣1|﹣|2x+1|的最大值为m．
（Ⅰ）作出函数f（x）的图象；
（Ⅱ）若a2+2c2+3b2=m，求ab+2bc的最大值．

【题目】已知函数f（x）=x2﹣alnx（a＞0）的最小值是1．
（Ⅰ）求a；
（Ⅱ）若关于x的方程f2（x）ex﹣6mf（x）+9me﹣x=0在区间[1，+∞）有唯一的实根，求m的取值范围．

【题目】已知椭圆 上两个不同的点A，B关于直线y=mx+ 对称．
（1）求实数m的取值范围；
（2）求△AOB面积的最大值（O为坐标原点）．

【题目】在△ABC中，a，b，c分别是角A，B，C的对边，且b，c是关于x的一元二次方程x2+mx﹣a2+b2+c2=0的两根．
（1）求角A的大小；
（2）已知a= ，设B=θ，△ABC的面积为y，求y=f（θ）的最大值．

【题目】已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜ ）的部分图象如图所示，将函数f（x）的图象向左平移m（m＞0）个单位后，得到的图象关于点（ ，﹣1）对称，则m的最小值是（ ）
A.
B.
C. π
D.

【题目】某批发市场对某种商品的周销售量（单位：吨）进行统计，最近100周的统计结果如下表所示：

周销售量

2

3

4

频数

20

50

30


（1）根据上面统计结果，求周销售量分别为2吨，3吨和4吨的频率；
（2）已知每吨该商品的销售利润为2千元，ξ表示该种商品两周销售利润的和（单位：千元），若以上述频率作为概率，且各周的销售量相互独立，求ξ的分布列和数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网