题目内容
14.已知函数$f(x)=\left\{\begin{array}{l}m{x^2}-8ax+n,x<1\\ log_a^x\begin{array}{l}{\begin{array}{l},{x≥1}\end{array}}\end{array}\end{array}\right.$,其中m为函数$g(x)=2x+\sqrt{x-1}$的最小值,n为函数$h(x)={3^{1-{x^2}}}$的最大值,且对任意x1≠x2,都有$\frac{{f({x_2})-f({x_1})}}{{{x_1}-{x_2}}}>0$成立,则实数a的取值范围是( )| A. | $(0,\frac{1}{2}]$ | B. | (1,2] | C. | $[\frac{5}{8},1)$ | D. | $[\frac{1}{2},\frac{5}{8}]$ |
分析 分别根据复合函数的单调性求出m,n的值,再由题意得到f(x)为减函数,根据二次函数和对数函数的性质即可求出a的取值范围.
解答 解:$g(x)=2x+\sqrt{x-1}$,x≥1,
设$\sqrt{x-1}$=t,t≥0,
则g(t)=2t2+t+2
∴g(t)[0,+∞)为增函数,
∴g(t)min=g(0)=2,
∴m=2,
∵y=1-x2在(-∞,0)为增函数,在(0,+∞)为减函数,
y=3x在R上为增函数
∴函数$h(x)={3^{1-{x^2}}}$在(-∞,0)为增函数,在(0,+∞)为减函数,
∴h(x)max=h(0)=3,
∴n=3,
∵对任意x1≠x2,都有$\frac{{f({x_2})-f({x_1})}}{{{x_1}-{x_2}}}>0$成立,
∴f(x)在R上为减函数,
∴当x≥1时,f(x)=logax为减函数,
∴0<a<1,
∵当x<1时,f(x)=2x2-8ax+3也为减函数,
∴$\frac{8a}{2×2}$≥1,
∴a≥$\frac{1}{2}$,
综上所述a的取值范围为(0,$\frac{1}{2}$],
故选:A.
点评 本题考查了复合函数的单调性,分段函数,函数的最值,参数耳朵取值范围,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.等差数列{an}、{bn}中的前n项和分别为Sn、Tn,$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n}{3n+1}$,则$\frac{{a}_{10}}{{b}_{10}}$=( )
| A. | $\frac{20}{31}$ | B. | $\frac{19}{29}$ | C. | $\frac{17}{28}$ | D. | $\frac{16}{27}$ |
2.椭圆$\frac{x^2}{m}+{y^2}$=1的一个焦点为$({\frac{1}{4},0})$,则m的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{17}{16}$ | C. | $\frac{1}{4}$ | D. | 4 |
9.有一个几何体的三视图及其尺寸如图(单位:cm),则该几何体的体积为( )
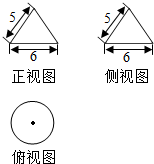

| A. | 12πcm3 | B. | 15πcm3 | C. | 24πcm3 | D. | 36πcm3 |
6.已知平面向量$\overrightarrow{a}$=(2cos2x,sin2x),$\overrightarrow{b}$=(cos2x,-2sin2x),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$ 要得到y=2cos(2x-$\frac{π}{6}$)的图象,只需要将y=f(x)的图象( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{12}$个单位 |