题目内容
17.若向量$\overrightarrow a=({2,t,-1})$,$\overrightarrow b=({-2,3,1})$,若$\overrightarrow a$与$\overrightarrow b$的夹角为钝角,则实数t的取值范围为$({-∞,-3})∪({-3,\frac{5}{3}})$.分析 由$\overrightarrow a$与$\overrightarrow b$的夹角为钝角,得到$cos<\overrightarrow{a},\overrightarrow{b}>$<0,且$cos<\overrightarrow{a},\overrightarrow{b}>$≠-1,由此能求出实数t的取值范围.
解答 解:∵向量$\overrightarrow a=({2,t,-1})$,$\overrightarrow b=({-2,3,1})$,$\overrightarrow a$与$\overrightarrow b$的夹角为钝角,
∴$cos<\overrightarrow{a},\overrightarrow{b}>$=$\frac{-4+3t-1}{\sqrt{5+{t}^{2}}•\sqrt{14}}$<0,且$cos<\overrightarrow{a},\overrightarrow{b}>$=$\frac{-4+3t-1}{\sqrt{5+{t}^{2}}•\sqrt{14}}$≠-1,
解得t<$\frac{5}{3}$,且t≠-3.
∴实数t的取值范围为$({-∞,-3})∪({-3,\frac{5}{3}})$.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意空间向量的数量积的性质的合理运用.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
8.下列各组中的函数相等的是( )
| A. | f(x)=$\sqrt{{x}^{2}}$,g(x)=($\sqrt{x}$)2 | B. | f(x)=|x|,g(x)=$\sqrt{{t}^{2}}$ | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=$\sqrt{x+1}-\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ |
2.椭圆$\frac{x^2}{m}+{y^2}$=1的一个焦点为$({\frac{1}{4},0})$,则m的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{17}{16}$ | C. | $\frac{1}{4}$ | D. | 4 |
9.有一个几何体的三视图及其尺寸如图(单位:cm),则该几何体的体积为( )
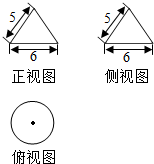

| A. | 12πcm3 | B. | 15πcm3 | C. | 24πcm3 | D. | 36πcm3 |
6.已知平面向量$\overrightarrow{a}$=(2cos2x,sin2x),$\overrightarrow{b}$=(cos2x,-2sin2x),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$ 要得到y=2cos(2x-$\frac{π}{6}$)的图象,只需要将y=f(x)的图象( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{12}$个单位 |
7.点A,B的坐标分别是(-5,0),(5,0),直线AM,BM相交于点M,且它们的斜率之积是$\frac{4}{9}$,则点M的轨迹方程是( )
| A. | $\frac{x^2}{25}+\frac{{9{y^2}}}{100}=1(x≠±5)$ | B. | $\frac{x^2}{25}+\frac{{100{y^2}}}{9}=1(x≠±5)$ | ||
| C. | $\frac{x^2}{25}-\frac{{9{y^2}}}{100}=1(y≠0)$ | D. | $\frac{x^2}{25}-\frac{{100{y^2}}}{9}=1(y≠0)$ |