题目内容
10.已知函数$f(x)={log_a}(1-\frac{2}{x+1})$(a>0,a≠1)(1)写出函数f(x)的值域、单调区间(不必证明)
(2)是否存在实数a使得f(x)的定义域为[m,n],值域为[1+logan,1+logam]?若存在,求出实数a的取值范围;若不存在说明理由.
分析 (1)由真数可以取到不等于1的所有正实数得函数的值域,分析出真数的单调性,由复合函数的单调性得到原函数的单调期间;
(2)假设存在实数a,使得f(x)的定义域为[m,n],值域为[1+logan,1+logam],可得0<a<1,问题转化为m,n是f(x)=1+logax的两根,进一步整理得到ax2+(a-1)x+1=0在(1,+∞)上有两不同解,然后利用三个二次结合得到关于a的不等式组,求解不等式组得答案.
解答 解:(1)∵$1-\frac{2}{x+1}$≠1,∴$lo{g}_{a}(1-\frac{2}{x+1})≠0$,
则$f(x)={log_a}(1-\frac{2}{x+1})$的值域为:(-∞,0)∪(0,+∞);
由$1-\frac{2}{x+1}>0$,解得x<-1或x>1,且1-$\frac{2}{x+1}$在(-∞,0)、(0,+∞)上为增函数,
∴当a>1时,f(x)的增区间:(-∞,-1),(1,+∞);
当0<a<1时,f(x)的减区间:(-∞,-1),(1,+∞);
(2)假设存在实数a,使得f(x)的定义域为[m,n],值域为[1+logan,1+logam],
由m<n,及1+logan<1+logam,得0<a<1,
∴f(m)=1+logam,f(n)=1+logan,
∴m,n是f(x)=1+logax的两根,
∴${log_a}(1-\frac{2}{X+1})=1+{log_a}x$,化简得ax2+(a-1)x+1=0在(1,+∞)上有两不同解,
设G(x)=ax2+(a-1)x+1,则$\left\{{\begin{array}{l}{G(1)>0}\\{-\frac{a-1}{2a}>1}\\{△>0}\end{array}}\right.$,解得$0<a<3-2\sqrt{2}$.
∴存在实数a∈(0,3-$2\sqrt{2}$),使得f(x)的定义域为[m,n],值域为[1+logan,1+logam].
点评 本题考查函数的定义域、值域及其求法,考查了复合函数的单调性,体现了分类讨论的数学思想方法和数学转化思想方法,是中档题.

| A. | $1-\frac{{\sqrt{3}}}{2},\frac{3}{2}$ | B. | $\frac{1}{2}$,$\frac{5}{4}$ | C. | $1-\frac{{\sqrt{3}}}{2},1+\frac{{\sqrt{3}}}{2}$ | D. | $1-\frac{{\sqrt{3}}}{2},1+\frac{{\sqrt{2}}}{2}$ |
| A. | a⊆A | B. | {a}⊆A | C. | a∉A | D. | {a}∈A |

| A. | $\overrightarrow{EF}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{CD}$ | B. | $\overrightarrow{EF}=-\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{CD}$ | C. | $\overrightarrow{EF}=\frac{1}{2}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{CD}$ | D. | $\overrightarrow{EF}=-\frac{1}{2}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{CD}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{17}{16}$ | C. | $\frac{1}{4}$ | D. | 4 |
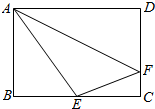 在矩形ABCD中,已知$AB=\sqrt{3},AD=2$,点E是BC的中点,点F在CD上,若$\overrightarrow{AB}•\overrightarrow{AF}$=$\sqrt{3}$,则$\overrightarrow{AE}•\overrightarrow{BF}$的值是$\sqrt{3}$-1.
在矩形ABCD中,已知$AB=\sqrt{3},AD=2$,点E是BC的中点,点F在CD上,若$\overrightarrow{AB}•\overrightarrow{AF}$=$\sqrt{3}$,则$\overrightarrow{AE}•\overrightarrow{BF}$的值是$\sqrt{3}$-1.