题目内容
(本小题满分12分)已知过点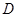
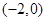 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 、
、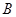 ,点
,点 是弦
是弦 的中点.
的中点.
(Ⅰ)若 ,求点
,求点 的轨迹方程;
的轨迹方程;
(Ⅱ)求 的取值范围.
的取值范围.
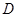
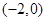 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 、
、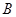 ,点
,点 是弦
是弦 的中点.
的中点.(Ⅰ)若
 ,求点
,求点 的轨迹方程;
的轨迹方程;(Ⅱ)求
 的取值范围.
的取值范围.(Ⅰ)点 的轨迹方程为
的轨迹方程为 (
(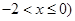 .(Ⅱ)
.(Ⅱ) .
.
 的轨迹方程为
的轨迹方程为 (
(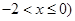 .(Ⅱ)
.(Ⅱ) .
.本试题主要是考查了圆锥曲线中轨迹方程的求解,以及直线与圆锥曲线的位置关系的综合而运用,研究线段的比值问题。
(1)根据题意点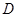
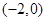 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 、
、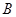 ,点
,点 是弦
是弦 的中点,且
的中点,且 ,设点
,设点 的坐标,利用直线与椭圆相交得到A,B点坐标关系式,从而的得到轨迹方程
的坐标,利用直线与椭圆相交得到A,B点坐标关系式,从而的得到轨迹方程
(2)利用直线方程与曲线方程联立,得到弦长公式,表示出线段比值。
解(Ⅰ)①若直线 ∥
∥ 轴,则点
轴,则点 为
为 ; ②设直线
; ②设直线 ,并设点
,并设点 的坐标分别是
的坐标分别是
 ,由
,由 消去
消去 ,得
,得  , ①
, ①
由直线 与椭圆有两个不同的交点,可得
与椭圆有两个不同的交点,可得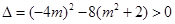 ,即
,即 ,所以
,所以 .
.
由 及方程①,得
及方程①,得 ,
,
 ,
,
即 由于
由于 (否则,直线
(否则,直线 与椭圆无公共点),将上方程组两式相除得,
与椭圆无公共点),将上方程组两式相除得, ,
,
代入到方程 ,得
,得 ,整理,得
,整理,得 (
( .
.
综上所述,点 的轨迹方程为
的轨迹方程为 (
(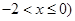 .
.
(Ⅱ)①当 ∥
∥ 轴时,
轴时, 分别是椭圆长轴的两个端点,则点
分别是椭圆长轴的两个端点,则点 在原点
在原点 处,所以,
处,所以,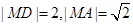 ,所以,
,所以, ; ②由方程①,得
; ②由方程①,得
所以, ,
,
 ,
,
所以 . 因为
. 因为 ,所以
,所以 ,所以
,所以 ,
,
所以 .综上所述,
.综上所述, .
.
(1)根据题意点
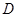
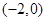 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 、
、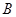 ,点
,点 是弦
是弦 的中点,且
的中点,且 ,设点
,设点 的坐标,利用直线与椭圆相交得到A,B点坐标关系式,从而的得到轨迹方程
的坐标,利用直线与椭圆相交得到A,B点坐标关系式,从而的得到轨迹方程(2)利用直线方程与曲线方程联立,得到弦长公式,表示出线段比值。
解(Ⅰ)①若直线
 ∥
∥ 轴,则点
轴,则点 为
为 ; ②设直线
; ②设直线 ,并设点
,并设点 的坐标分别是
的坐标分别是 ,由
,由 消去
消去 ,得
,得  , ①
, ①由直线
 与椭圆有两个不同的交点,可得
与椭圆有两个不同的交点,可得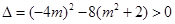 ,即
,即 ,所以
,所以 .
. 由
 及方程①,得
及方程①,得 ,
, ,
,即
 由于
由于 (否则,直线
(否则,直线 与椭圆无公共点),将上方程组两式相除得,
与椭圆无公共点),将上方程组两式相除得, ,
,代入到方程
 ,得
,得 ,整理,得
,整理,得 (
( .
.综上所述,点
 的轨迹方程为
的轨迹方程为 (
(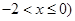 .
.(Ⅱ)①当
 ∥
∥ 轴时,
轴时, 分别是椭圆长轴的两个端点,则点
分别是椭圆长轴的两个端点,则点 在原点
在原点 处,所以,
处,所以,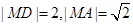 ,所以,
,所以, ; ②由方程①,得
; ②由方程①,得
所以,
 ,
, ,
,所以
 . 因为
. 因为 ,所以
,所以 ,所以
,所以 ,
,所以
 .综上所述,
.综上所述, .
.
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 :
: ,a,b为常数),动圆
,a,b为常数),动圆 ,
, 。点
。点 分别为
分别为 与
与 与直线
与直线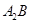 交点M的轨迹方程;
交点M的轨迹方程; 与
与 四点,其中
四点,其中 ,
, 。若矩形
。若矩形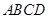 与矩形
与矩形 的面积相等,证明:
的面积相等,证明: 为定值。
为定值。
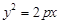 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( ) 倍后得到点Q(x,
倍后得到点Q(x, ·
· ="1."
="1."  的直线L交曲线C于M、N两点,且
的直线L交曲线C于M、N两点,且 +
+ +
+ =
= ,试求△MNH的面积.
,试求△MNH的面积. 分别为椭圆
分别为椭圆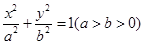 的左、右顶点,若在椭圆上存在异于
的左、右顶点,若在椭圆上存在异于 ,使得
,使得 ,其中
,其中 为坐标原点,则椭圆的离心率
为坐标原点,则椭圆的离心率 的取值范围是
的取值范围是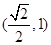


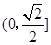
 ,
, ,曲线
,曲线 上的动点
上的动点 满足
满足 ,直线
,直线 与曲线
与曲线 .
. ,若
,若
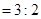 ,求直线
,求直线 的方程.
的方程. 的离心率为
的离心率为 ,点
,点 ,
,  为
为 上两点,斜率为
上两点,斜率为 的直线与椭圆
的直线与椭圆 交于点
交于点 ,
, (
( 两侧).
两侧).
 面积的最大值;
面积的最大值; ,
, 的斜率为
的斜率为 ,试判断
,试判断 是否为定值.若是,求出这个定值;若不是,说明理由.
是否为定值.若是,求出这个定值;若不是,说明理由.  定点
定点 ,点
,点 为圆
为圆 上的动点,点
上的动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 。
。 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由。
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由。 的曲线恰好有两个不同的公共点,则实数
的曲线恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是

