题目内容
（本小题满分14分）
已知椭圆
的离心率为
，点
， 
为
上两点，斜率为
的直线与椭圆
交于点
，
（，在直线
两侧）．
（I）求四边形
面积的最大值；
（II）设直线
，
的斜率为
，试判断
是否为定值．若是，求出这个定值；若不是，说明理由．
已知椭圆
的离心率为，点， 为上两点，斜率为的直线与椭圆交于点，（，在直线两侧）．（I）求四边形
面积的最大值；（II）设直线
，的斜率为，试判断是否为定值．若是，求出这个定值；若不是，说明理由． （1）
=
；（2）
为定值.
=；（2）为定值.（I）
，设椭圆
，将点
代入椭圆，得
，
所以椭圆的方程为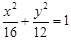
…………2分
设直线的方程为
，
，得
则
,
…………4分
又
=
显然当
时, = …………6分
（II）设直线
、
的方程分别为
（5） 
（
）
将（5）代入（4）得：
则
…………8分
同理：
…………10分
化简得：
即为定值。 …………12分
，设椭圆，将点代入椭圆，得，所以椭圆
的方程为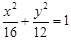 …………2分设直线的方程为
，，得则
, …………4分又
=
显然当
时, = …………6分（II）设直线
、的方程分别为 （5） （）将（5）代入（4）得：
则 …………8分 同理： …………10分化简得：
即
为定值。 …………12分
练习册系列答案
阅读快车系列答案
相关题目
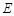的两焦点分别为
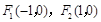，且椭圆上的点到
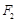的最小距离为
.
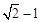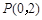作直线
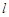交椭圆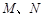
两点，设线段
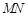的中垂线交
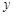轴于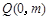
，求m的取值范围.
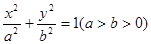的左焦点
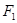作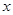
轴的垂线交椭圆于点
,
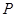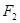为右焦点,若
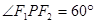,则椭圆的离心率为__________________ ．
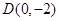作抛物线 
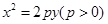的切线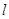
，切点A在第二象限.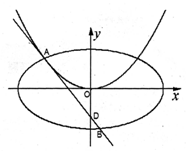
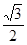的椭圆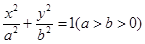
恰好经过切点A，设切线
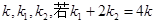，求椭圆方程．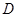
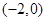的直线
与椭圆
交于不同的两点
、
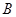，点
是弦
的中点．
，求点
的轨迹方程；
的取值范围．
，焦点在
轴上，离心率为
，且椭圆E上一点到两个焦点距离之和为4；
，
是过点
且相互垂直的两条直线，
，
两点，
，
两点，
，
的中点分别为
，
．
的取值范围；
与直线
的斜率乘积为定值．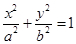
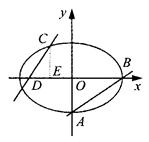
（a＞b＞0）的离心率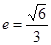
，过点A（0，-b）和B（a，0）的直线与原点的距离为
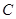的极坐标方程是ρ=2，以极点为原点，极轴为
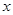轴的正半轴建立平面直角坐标系
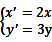后得到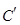曲线
，求曲线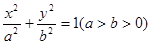
的左、右焦点分别为
，线段
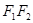被抛物线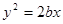
的焦点F分成5:3两段，则椭圆的离心率为 ( ）
