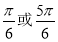题目内容
7.已知命题p:|x-1|+|x+1|≥3a恒成立,命题q:y=(2a-1)x为减函数.(1)若命题p为真命题,求实数a的取值范围.
(2)若命题q为真命题,求实数a的取值范围.
(3)若“p∧q”为真命题.求实数a的取值范围.
(4)若“p∨q”与“?p∨?q”都为真命题,求实数a的取值范围.
分析 (1)利用绝对值的几何意义求解即可.
(2)利用指数函数的性质写出结果即可.
(3)两个命题都是真命题,求解交集即可.
(4)两个命题一真一假,求解即可.
解答 解:(1)∵|x-1|+|x+1|≥|(x-1)-(x+1)|=2,p真 2≥3a,$a≤\frac{2}{3}$…(3分)
(2)q真,命题q:y=(2a-1)x为减函数,0<2a-1<1,∴$\frac{1}{2}<a<1$…(6分)
(3)p真,$a≤\frac{2}{3}$,q真,$\frac{1}{2}<a<1$,“p∧q”为真命题.可得$\frac{1}{2}<a≤\frac{2}{3}$…(9分)
(4)p∨q与?p∨?q都为真,p,q一真一假 $a≤\frac{1}{2}$或$\frac{2}{3}<a<1$…(12分)
点评 本题考查命题的真假的判断与应用,考查计算能力.

练习册系列答案
相关题目
18.设log89=a,log35=b,则lg2=( )
| A. | $\frac{2}{2+3ab}$ | B. | $\frac{1-a}{2ab}$ | C. | $\frac{1-a}{a+2b}$ | D. | $\frac{1-a}{{a}^{2}+b}$ |
15.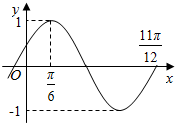 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
15.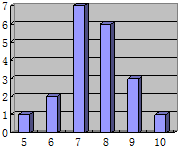 某射击小组有20个人,教练根据他们某次射击的数据绘制成如图的统计图,则这组数据的众数和中位数分别是( )
某射击小组有20个人,教练根据他们某次射击的数据绘制成如图的统计图,则这组数据的众数和中位数分别是( )
 某射击小组有20个人,教练根据他们某次射击的数据绘制成如图的统计图,则这组数据的众数和中位数分别是( )
某射击小组有20个人,教练根据他们某次射击的数据绘制成如图的统计图,则这组数据的众数和中位数分别是( )| A. | 7,7 | B. | 8,7.5 | C. | 7,7.5 | D. | 8,6 |
16.已知a>0,b<0,则“a+b=0”是“a+b≥2ab”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 中,角
中,角 所对的边分别为
所对的边分别为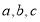 .若
.若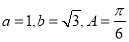 ,则角
,则角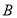 等于( )
等于( )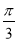 B.
B.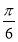 C.
C.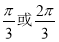 D.
D.