题目内容
19．x为实数，[x]表示不超过x的最大整数，则函数f（x）=x-[x]的最小正周期是1．分析 当x∈[0，1）时，画出函数f（x）=x-[x]的图象，再左右扩展知f（x）为周期函数．由此利用数形结合思想能求出函数f（x）=x-[x]的最小正周期．
解答 解：∵x为实数，[x]表示不超过x的最大整数，
∴如图，当x∈[0，1）时，画出函数f（x）=x-[x]的图象，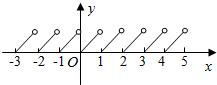
再左右扩展知f（x）为周期函数．
结合图象得到函数f（x）=x-[x]的最小正周期是1．
故答案为：1．
点评 本题考查函数的最小正周期的求法，是基础题，解题时要认真审题，注意数形结合思想的合理运用．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
10．设函数f（x）=ex+x-2，g（x）=lnx+x2-1，若实数a，b满足f（a）=0，g（b）=0，则（ ）
| A． | g（a）＜0＜f（b） | B． | f（b）＜0＜g（a） | C． | 0＜g（a）＜f（b） | D． | f（b）＜g（a）＜0 |
10．已知F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，若在双曲线的右支上存在一点M，使得（$\overrightarrow{OM}$+$\overrightarrow{O{F}_{2}}$）•$\overrightarrow{{F}_{2}M}$=0 （其中O为坐标原点），且|$\overrightarrow{M{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{M{F}_{2}}$|，则双曲线的离心率为（ ）
| A． | $\sqrt{5}$-1 | B． | $\frac{\sqrt{3}+1}{2}$ | C． | $\frac{\sqrt{5}+1}{2}$ | D． | $\sqrt{3}$+1 |
3．设函数f（x）=$\left\{\begin{array}{l}{3x-b，x＜1}\\{{2}^{x}，x≥1}\end{array}\right.$，若f[f（$\frac{1}{3}$）]=4，则b=（ ）
| A． | 1 | B． | -$\frac{1}{4}$ | C． | -$\frac{1}{4}$或1 | D． | -1 |
7．设函数f（x），g（x）的定义域为R，且f（x）是奇函数，g（x）是偶函数，则下列结论中正确的是（ ）
| A． | f（x）g（x）是偶函数 | B． | |f（x）|g（x） 是奇函数 | C． | |f（x）g（x）|是奇函数 | D． | f（|x|）是偶函数 |