题目内容
如图所示,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合,求形成的三棱锥的外接球的体积.

外接球体积为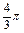 ×OA3=
×OA3=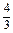 ·
·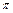 ·
·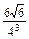 =
=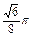
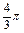 ×OA3=
×OA3=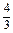 ·
·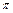 ·
·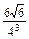 =
=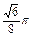
由已知条件知,平面图形中AE=EB=BC=CD=DA=DE=EC=1
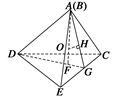
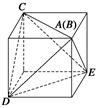
∴折叠后得到一个正四面体. 2分
方法一 作AF⊥平面DEC,垂足为F,F即为△DEC的中心.
取EC的中点G,连接DG、AG,
过球心O作OH⊥平面AEC.
则垂足H为△AEC的中心. 4分
∴外接球半径可利用△OHA∽△GFA求得.
∵AG=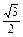 ,AF=
,AF=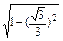 =
=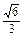 , 6分
, 6分
在△AFG和△AHO中,根据三角形相似可知,
AH=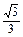 .∴OA=
.∴OA=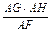 =
=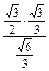 =
=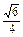 . 10分
. 10分
∴外接球体积为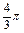 ×OA3=
×OA3=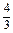 ·
·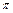 ·
·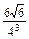 =
=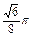 . 14分
. 14分
方法二 如图所示,把正四面体放在正方体中.显然,正四面体
的外接球就是正方体的外接球. 6分
∵正四面体的棱长为1,
∴正方体的棱长为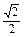 ,∴外接球直径2R=
,∴外接球直径2R=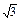 ·
·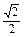 , 10分
, 10分
∴R=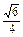 ,∴体积为
,∴体积为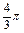 ·
·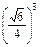 =
=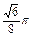 . 12分
. 12分
∴该三棱锥外接球的体积为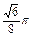 . 14分
. 14分


∴折叠后得到一个正四面体. 2分
方法一 作AF⊥平面DEC,垂足为F,F即为△DEC的中心.
取EC的中点G,连接DG、AG,
过球心O作OH⊥平面AEC.
则垂足H为△AEC的中心. 4分
∴外接球半径可利用△OHA∽△GFA求得.
∵AG=
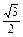 ,AF=
,AF=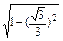 =
=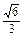 , 6分
, 6分在△AFG和△AHO中,根据三角形相似可知,
AH=
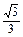 .∴OA=
.∴OA=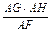 =
=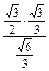 =
=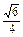 . 10分
. 10分∴外接球体积为
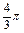 ×OA3=
×OA3=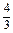 ·
·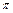 ·
·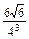 =
=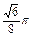 . 14分
. 14分方法二 如图所示,把正四面体放在正方体中.显然,正四面体
的外接球就是正方体的外接球. 6分
∵正四面体的棱长为1,
∴正方体的棱长为
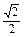 ,∴外接球直径2R=
,∴外接球直径2R=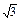 ·
·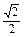 , 10分
, 10分∴R=
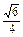 ,∴体积为
,∴体积为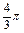 ·
·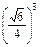 =
=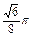 . 12分
. 12分∴该三棱锥外接球的体积为
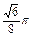 . 14分
. 14分
练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
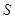 ,则圆柱的体积为( ).
,则圆柱的体积为( ).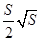
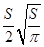
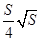

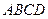 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛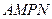 ,要求
,要求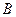 点在
点在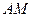 上,
上,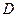 点在
点在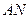 上,且对角线
上,且对角线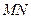 过
过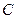 点,已知
点,已知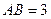 米,
米,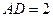 米.
米.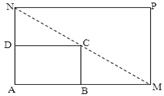
 的长应在什么范围内?
的长应在什么范围内?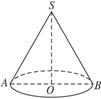


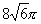 B.
B.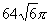 C.
C.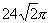 D.
D.