题目内容
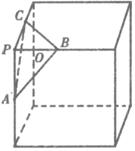
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则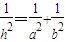 ,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M=
,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M=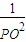 ,N=
,N=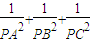 ,那么M、N的大小关系是 .
,那么M、N的大小关系是 .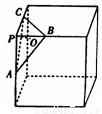
【答案】分析:由题意Rt△ABC中两直角边为a、b,斜边c上的高为h,由等面积法得ch=ab,c2•h2=a2•b2,然后再利用等体积法进行比较.
解答:解:在Rt△ABC中,c2=a2+b2①,由等面积法得ch=ab,
∴c2•h2=a2•b2②,①÷②整理得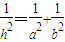 .
.
类比得,S△ABC2=S△PAB2+S△PBC2+S△PAC2①,
由等体积法得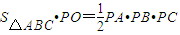 ,
,
∴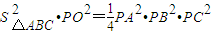 ②,
②,
①÷②整理得M=N.
故答案为:M=N.
点评:此题考查直角三角形的性质及等面积法和等体积法的应用,是一道基础题.
解答:解:在Rt△ABC中,c2=a2+b2①,由等面积法得ch=ab,
∴c2•h2=a2•b2②,①÷②整理得
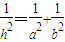 .
.类比得,S△ABC2=S△PAB2+S△PBC2+S△PAC2①,
由等体积法得
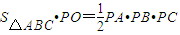 ,
,∴
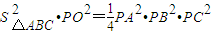 ②,
②,①÷②整理得M=N.
故答案为:M=N.
点评:此题考查直角三角形的性质及等面积法和等体积法的应用,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则