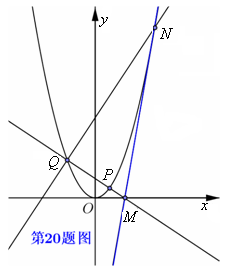
题目内容
直线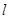 与抛物线
与抛物线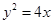 交于
交于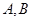 两点,
两点, 为原点,如果
为原点,如果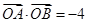 ,那么直线
,那么直线 恒经过定点
恒经过定点 的坐标为__________________
的坐标为__________________
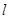 与抛物线
与抛物线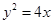 交于
交于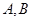 两点,
两点,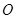 为原点,如果
为原点,如果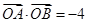 ,那么直线
,那么直线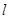 恒经过定点
恒经过定点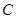 的坐标为__________________
的坐标为__________________
设l:y=kx+b A(x1,y1) B(x2,y2)
k^2x^2+[2kb-4]x+b^2=0 x1 x2=b^2/k^2 x1+ x2 =[4-2kb]/k^2
OA*OB= x1 x2+ y1 y2=(1+k^2)x1x2+bk(x1+x2)+b^2=-4 b^2+4kb+4k^2=0
b=-2k
y=kx+b=kx-2k=k(x-2) C是(2,0)
k^2x^2+[2kb-4]x+b^2=0 x1 x2=b^2/k^2 x1+ x2 =[4-2kb]/k^2
OA*OB= x1 x2+ y1 y2=(1+k^2)x1x2+bk(x1+x2)+b^2=-4 b^2+4kb+4k^2=0
b=-2k
y=kx+b=kx-2k=k(x-2) C是(2,0)

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 是抛物线
是抛物线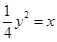 上一个动点,则点
上一个动点,则点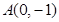 的距离与点
的距离与点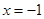 的距离和的最小值是 。
的距离和的最小值是 。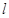 过抛物线
过抛物线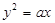 的焦点F,且与
的焦点F,且与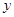 轴相交于点A,若
轴相交于点A,若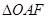
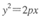 的焦点为F,点A、B、C在此抛物线上,点A坐标为(1, 2).若点F恰为
的焦点为F,点A、B、C在此抛物线上,点A坐标为(1, 2).若点F恰为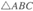 的重心,则直线BC的方程为
的重心,则直线BC的方程为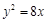 相交于A、B两点,F为C的焦点,若
相交于A、B两点,F为C的焦点,若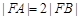 ,则
,则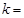 ( )
( )
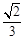
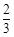
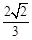
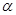 的直线经过抛物线
的直线经过抛物线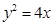 的焦点,且与抛物线交于A、B两点,Q为A、B中点,
的焦点,且与抛物线交于A、B两点,Q为A、B中点,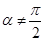 ,作线段AB的垂直平分线
,作线段AB的垂直平分线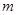 交x轴于点P,证明:|AB|=2|PF|。
交x轴于点P,证明:|AB|=2|PF|。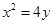 ,过定点
,过定点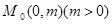 的直线
的直线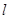 交抛物线于A、B两点.
交抛物线于A、B两点.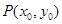 在定直线
在定直线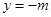 上.
上. 时,在抛物线上存在不同的两点P、Q关于直线
时,在抛物线上存在不同的两点P、Q关于直线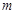 表示),若不存在,请说明理由.
表示),若不存在,请说明理由.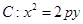 (
(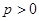 )上一点
)上一点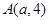 到其准线的距离为
到其准线的距离为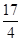 .
.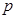 与
与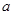 的值;
的值;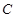 上动点
上动点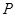 的横坐标为
的横坐标为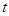 (
(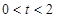 ),过点
),过点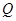 ,交
,交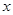 轴于
轴于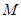 点(直线
点(直线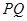 的斜率记作
的斜率记作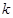 ).过点
).过点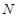 .若
.若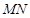 恰好是
恰好是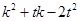 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.