题目内容
(本小题共8分)
提高二环路的车辆通行能力可有效改善整个城区的交通状况,在一般情况下,二环路上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数。当二环路上的车流密度达到600辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过60辆/千米时,车流速度为80千米/小时,研究表明:当60≤x≤600时,车流速度v是车流密度x的一次函数。
(Ⅰ)当0≤x≤600时,求函数f(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过二环路上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值。(精确到1辆/小时)
(1) f(x)= 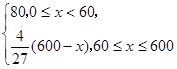
(2) 当车流密度为300辆/千米时,车流量达到最大值,约为13333辆/小时.
解析试题分析:解:(Ⅰ)由题意:当0≤x≤60时,v(x)=80;
当60≤x≤600时,设v(x)=ax+b,显然v(x)=ax+b在[60,600]是减函数,
由已知得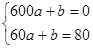 ,解得
,解得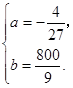
故函数v(x)的表达式为v(x)=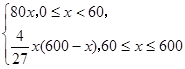 4分
4分
(Ⅱ)依题意并由(Ⅰ)可得f(x)= 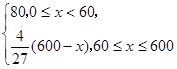
当0≤x≤60时,f(x)为增函数,故当x=60时,其最大值为60×80=4800;
当60≤x≤600时,f(x)=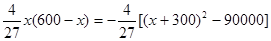 ≤
≤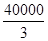 ,
,
当且仅当x=300时,等号成立.
所以,当x=300时,f(x)在区间[60,600]上取得最大值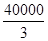 .
.
综上,当x=300时,f(x)在区间[0,600]上取得最大值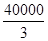 ≈13333,
≈13333,
即当车流密度为300辆/千米时,车流量达到最大值,约为13333辆/小时. 8分
考点:函数的实际运用
点评:解决该试题的关键是对于实际问题能翻译为代数式,同时能结合函数的性质得到最值。属于基础题。

练习册系列答案
相关题目
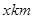 ,建在C处的垃圾处理厂对城A和城B的总影响度为
,建在C处的垃圾处理厂对城A和城B的总影响度为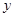 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。

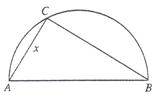
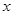 的函数;
的函数; (2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
 ,其中
,其中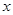 是仪器的月产量
是仪器的月产量 表示为月产量
表示为月产量 BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
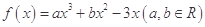 在点
在点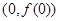 处的切线与直线
处的切线与直线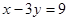 垂直.
垂直.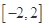 上任意两个自变量的值
上任意两个自变量的值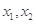 都有
都有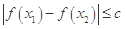 ,求实数
,求实数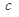 的最小值;
的最小值;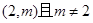 可作曲线
可作曲线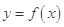 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围. 。
。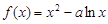 在
在 是增函数,
是增函数,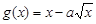 在(0,1)为减函数.
在(0,1)为减函数.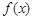 、
、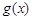 的表达式;
的表达式;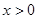 时,方程
时,方程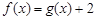 有唯一解;
有唯一解;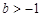 时,若
时,若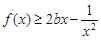 在
在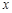 ∈
∈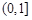 内恒成立,求
内恒成立,求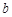 的取值范围.
的取值范围.