题目内容
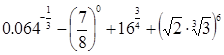 。
。
81.5
解析试题分析:解:(1)原式= =2.5-1+8+72
=2.5-1+8+72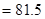 7分
7分
考点:本题主要考查有理指数幂的运算。
点评:简单题,牢记运算法则,细心计算。应用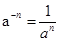 。
。

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
题目内容
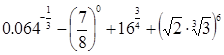 。
。
81.5
解析试题分析:解:(1)原式= =2.5-1+8+72
=2.5-1+8+72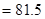 7分
7分
考点:本题主要考查有理指数幂的运算。
点评:简单题,牢记运算法则,细心计算。应用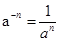 。
。

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案