题目内容
9.已知实数m是2和8的等比中项,则抛物线y=mx2的焦点坐标为(0,±$\frac{1}{16}$).分析 由等比中项概念求得m的值,代入抛物线方程,分m=4和m=-4求得抛物线的焦点坐标.
解答 解:∵实数m是2和8的等比中项,
∴m2=16,m=±4,
由y=mx2,得${x}^{2}=\frac{1}{m}y$,
若m=4,则${x}^{2}=\frac{1}{4}y$,即2p=$\frac{1}{4}$,$\frac{p}{2}=\frac{1}{16}$,焦点坐标为(0,$\frac{1}{16}$);
若m=-4,则${x}^{2}=-\frac{1}{4}$,即2p=$\frac{1}{4}$,$\frac{p}{2}=\frac{1}{16}$,焦点坐标为(0,-$\frac{1}{16}$).
∴抛物线y=mx2的焦点坐标为:(0,±$\frac{1}{16}$).
故答案为:(0,±$\frac{1}{16}$).
点评 本题考查了等比中项的概念,考查了抛物线的简单几何性质,属中档题.

练习册系列答案
相关题目
17.已知x∈(0,1),a=$\frac{sinx}{x}$,b=$\frac{sin{x}^{3}}{{x}^{3}}$,c=$\frac{si{n}^{3}x}{{x}^{3}}$,则a,b,c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
4.某校开设A类选修课2门,B类选修课3门,一位同学从中选3门.若要求两类课程中各至少选一门,则不同的选法共有( )
| A. | 3种 | B. | 6种 | C. | 9种 | D. | 18种 |
14.对任意非零实数a、b,若a?b的运算原理如图所示,则log24?($\frac{1}{3}$)-1的值为( )


| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
1.下列说法错误的是( )
| A. | 已知两个命题p,q,若p∧q为假命题,则p∨q也为假命题 | |
| B. | 实数a=0是直线ax-2y=1与2ax-2y=3平行的充要条件 | |
| C. | “存在x∈R,使得x2+2x+5=0”的否定是“对任何x∈R,都有x2+2x+5≠0 | |
| D. | 命题p:?x∈R,x2+1≥1;命题q:?x∈R,x2-x+1≤0,则命题p∧(¬q)是真命题 |
17.在复平面内,复数$\frac{2-3i}{i^3}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.已知函数f(x)=sinx-a,(0≤x≤$\frac{5π}{2}$)的三个零点成等比数列,则a=( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
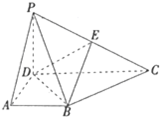 在四棱锥PABCD中,侧面PCD⊥底面ABCD,PD⊥CD,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4
在四棱锥PABCD中,侧面PCD⊥底面ABCD,PD⊥CD,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4