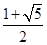题目内容
设F1,F2分别是双曲线 =1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使(
=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使( +
+ )·
)· =0,O为坐标原点,且
=0,O为坐标原点,且 =
= |
| |,则双曲线的离心率为( ).
|,则双曲线的离心率为( ).
A. +1 +1 | B. | C. | D.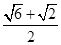 |
A
解析

练习册系列答案
相关题目
一个酒杯的轴截面是抛物线的一部分,它的方程是 .在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围是( )
.在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围是( )
| A.0<r≤1 | B.0<r<1 | C.0<r≤2 | D.0<r<2 |
已知双曲线 与椭圆
与椭圆 的离心率互为倒数,则双曲线的渐近线方程为( )
的离心率互为倒数,则双曲线的渐近线方程为( )
A. | B. | C. | D. |
已知椭圆
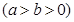 的离心率
的离心率 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根
的两个实根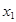 ,
,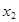 ,则点
,则点 ( )
( )
A.必在圆 内 内 | B.必在圆 上 上 |
C.必在圆 外 外 | D.以上三种情况都有可能 |
若 ,则方程
,则方程 表示( )
表示( )
A.焦点在 轴上的椭圆 轴上的椭圆 | B.焦点在 轴上的椭圆 轴上的椭圆 |
C.焦点在 轴上的双曲线 轴上的双曲线 | D.焦点在 轴上的双曲线 轴上的双曲线 |
已知双曲线 的顶点恰好是椭圆
的顶点恰好是椭圆 的两个顶点,且焦距是
的两个顶点,且焦距是 ,则此双曲线的渐近线方程是( )
,则此双曲线的渐近线方程是( )
A. | B. | C. | D. |
已知双曲线C1: =1(a>0,b>0)的离心率为2,若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( ).
=1(a>0,b>0)的离心率为2,若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( ).
A.x2= y y | B.x2= y y |
| C.x2=8y | D.x2=16y |
若点O和点F分别为椭圆 的中心和左焦点,点P为椭圆上任意一点,则
的中心和左焦点,点P为椭圆上任意一点,则 的最大值 ( ).
的最大值 ( ).
| A.2 | B.3 | C.6 | D.8 |
 ,则双曲线的离心率为( ).
,则双曲线的离心率为( ).