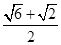题目内容
若 ,则方程
,则方程 表示( )
表示( )
A.焦点在 轴上的椭圆 轴上的椭圆 | B.焦点在 轴上的椭圆 轴上的椭圆 |
C.焦点在 轴上的双曲线 轴上的双曲线 | D.焦点在 轴上的双曲线 轴上的双曲线 |
B
解析试题分析:因为椭圆的标准方程为 ,又
,又 ,所以可得
,所以可得 .即椭圆的长轴在y轴上,所以椭圆的焦点在y轴上,故选B.本小题关键椭圆的焦点在那个轴上的问题,首先是化为标准方程后根据
.即椭圆的长轴在y轴上,所以椭圆的焦点在y轴上,故选B.本小题关键椭圆的焦点在那个轴上的问题,首先是化为标准方程后根据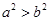 .确定在那个轴上.
.确定在那个轴上.
考点:1.椭圆的标准方程.2.椭圆的性质.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
已知双曲线 的一条渐近线方程是
的一条渐近线方程是 ,它的一个焦点在抛物线
,它的一个焦点在抛物线 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为
A. | B. |
C. | D. |
已知 ,
, ,
, ,则动点
,则动点 的轨迹是( )
的轨迹是( )
| A.双曲线 | B.圆 | C.椭圆 | D.抛物线 |
设 为抛物线
为抛物线 的焦点,
的焦点, 为该抛物线上三点,若
为该抛物线上三点,若 ,则
,则 的值为 ( )
的值为 ( )
A. | B. | C. | D.12 |
设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( ).
| A.y2=4x或y2=8x | B.y2=2x或y2=8x |
| C.y2=4x或y2=16x | D.y2=2x或y2=16x |
 :
:
 的焦点与双曲线
的焦点与双曲线 :
: 的左焦点的连线交
的左焦点的连线交 .若
.若 ( )
( )



 上一点
上一点 ,过双曲线中心的直线交双曲线于
,过双曲线中心的直线交双曲线于 两点,记直线
两点,记直线 的斜率分别为
的斜率分别为 ,当
,当 最小时,双曲线离心率为( )
最小时,双曲线离心率为( ) B.
B. C
C D
D
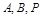 是双曲线
是双曲线 上不同的三点,且
上不同的三点,且 连线经过坐标原点,若直线
连线经过坐标原点,若直线 的斜率乘积
的斜率乘积 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )



 =1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使(
=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使( +
+ )·
)· =0,O为坐标原点,且
=0,O为坐标原点,且 =
= |
| |,则双曲线的离心率为( ).
|,则双曲线的离心率为( ).