题目内容
【题目】已知正项数列![]() 的前n项和
的前n项和![]() 满足
满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若 (n∈N*),求数列
(n∈N*),求数列![]() 的前n项和
的前n项和![]() ;
;
(3)是否存在实数![]() 使得
使得![]() 对
对![]() 恒成立,若存在,求实数
恒成立,若存在,求实数![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)根据![]() 与
与![]() 的关系
的关系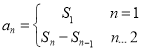 ,即可求出
,即可求出![]() 的通项公式;
的通项公式;
(2)由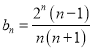 ,可采用裂项相消法求数列
,可采用裂项相消法求数列![]() 的前n项和
的前n项和![]() ;
;
(3)假设存在实数λ,使得![]() 对一切正整数恒成立,
对一切正整数恒成立,
即![]() 对一切正整数恒成立,只需满足
对一切正整数恒成立,只需满足![]() 即可,利用作差法得出
即可,利用作差法得出![]() 其单调性,即可求解.
其单调性,即可求解.
(1)当n=1时,a1=2或-1(舍去).
当n≥2时,![]() ,
,
整理可得:(an+an-1)(an-an-1-1)=0,可得an-an-1=1,
∴{an}是以a1=2为首项,d=1为公差的等差数列.∴![]() .
.
(2)由(1)得an=n+1,∴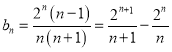 .
.
∴ .
.
(3)假设存在实数λ,使得![]() 对一切正整数恒成立,
对一切正整数恒成立,
即![]() 对一切正整数恒成立,只需满足
对一切正整数恒成立,只需满足![]() 即可,
即可,
令![]() ,则
,则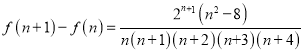
当![]()
故f(1)=1,f(2)=![]() ,f(3)=
,f(3)=![]() ,
,![]() >f(5)>f(6)>…
>f(5)>f(6)>…
当n=3时有最小值![]() ,所以
,所以![]() .
.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目