题目内容
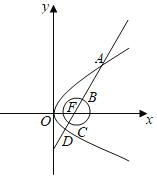
【题目】(本题满分12分)已知椭圆![]() ,直线
,直线![]() 不过原点
不过原点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)证明:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
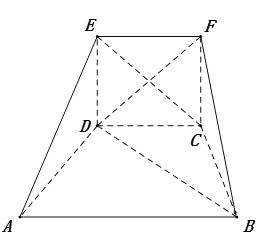
(Ⅱ)若![]() 过点
过点![]() ,延长线段
,延长线段![]() 与
与![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求此时
能否为平行四边形?若能,求此时![]() 的斜率,若不能,说明理由.
的斜率,若不能,说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)能,![]() 或
或![]() .
.
【解析】
试题分析:(1)设直线![]()
![]() ,直线方程与椭圆方程联立,根据韦达定理求根与系数的关系,并表示直线
,直线方程与椭圆方程联立,根据韦达定理求根与系数的关系,并表示直线![]() 的斜率,再表示
的斜率,再表示![]() ;
;
(2)第一步由 (Ⅰ)得![]() 的方程为
的方程为![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,直线
,直线![]() 与椭圆方程联立求点
与椭圆方程联立求点![]() 的坐标,第二步再整理点
的坐标,第二步再整理点![]() 的坐标,如果能构成平行四边形,只需
的坐标,如果能构成平行四边形,只需![]() ,如果有
,如果有![]() 值,并且满足
值,并且满足![]() ,
,![]() 的条件就说明存在,否则不存在.
的条件就说明存在,否则不存在.
试题解析:解:(1)设直线![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴由![]() 得
得![]() ,
,
∴![]() ,
,![]() .
.
∴直线![]() 的斜率
的斜率![]() ,即
,即![]() .
.
即直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值
的斜率的乘积为定值![]() .
.
(2)四边形![]() 能为平行四边形.
能为平行四边形.
∵直线![]() 过点
过点![]() ,∴
,∴![]() 不过原点且与
不过原点且与![]() 有两个交点的充要条件是
有两个交点的充要条件是![]() ,
,![]()
由 (Ⅰ)得![]() 的方程为
的方程为![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
∴由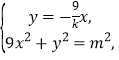 得
得![]() ,即
,即![]()
将点![]() 的坐标代入直线
的坐标代入直线![]() 的方程得
的方程得![]() ,因此
,因此![]() .
.
四边形![]() 为平行四边形当且仅当线段
为平行四边形当且仅当线段![]() 与线段
与线段![]() 互相平分,即
互相平分,即![]()
∴![]()
![]() .解得
.解得![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴当![]() 的斜率为
的斜率为![]() 或
或![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
【题目】某商家对他所经销的一种商品的日销售量(单位:吨)进行统计,最近50天的统计结果
如下表:
日销售量 | 1 | 1.5 | 2 |
天数 | 10 | 25 | 15 |
频率 | 0.2 |
|
|
若以上表中频率作为概率,且每天的销售量相互独立.
(1)求5天中该种商品恰好有两天的销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元,表示该种商品某两天销售利润的和(单位:千元),求的分布列和数学期望.