题目内容
1．函数y=tan2x的值域为R．分析 由条件根据正切函数的图象特征，可得结论．
解答 解：根据正切函数的图象可得函数y=tan2x的值域为R，
故答案为：R．
点评 本题主要考查正切函数的图象特征，属于基础题．
练习册系列答案
通城学典默写能手系列答案
相关题目
11．
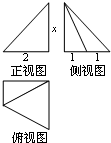某几何体的三视图如图所示，且该几何体的体积是6，则正视图中的x的值是（ ）
某几何体的三视图如图所示，且该几何体的体积是6，则正视图中的x的值是（ ）| A． | 9 | B． | 8 | C． | 3 | D． | 6 |
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．
在极坐标系中，已知圆C的圆心在点C（2，0）且经过极点O，点P（6，0）．
10．已知椭圆的焦点在x轴上，短轴长为2，离心率为$\frac{\sqrt{3}}{2}$，直线l：y=-2，任取椭圆上一点P（异于短轴端点M，N）直线MP，NP分别交直线l于点T，S，则|ST|的最小值是（ ）
| A． | 2$\sqrt{3}$ | B． | 4$\sqrt{2}$ | C． | 4$\sqrt{3}$ | D． | 8$\sqrt{2}$ |