题目内容
(本小题满分12分)
已知函数f(x)=4x3-3x2sin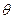 +
+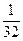 的极小值大于零,其中x∈R,
的极小值大于零,其中x∈R, 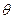 ∈[0,
∈[0,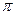 ].
].
(1).求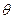 的取值范围.
的取值范围.
(2).若在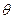 的取值范围内的任意
的取值范围内的任意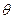 ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
(3).设x0>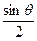 ,f(x0) >
,f(x0) >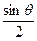 ,若f[f(x0)]=x0,求证f(x0)=x0
,若f[f(x0)]=x0,求证f(x0)=x0
已知函数f(x)=4x3-3x2sin
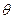 +
+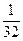 的极小值大于零,其中x∈R,
的极小值大于零,其中x∈R, 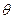 ∈[0,
∈[0,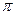 ].
].(1).求
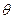 的取值范围.
的取值范围.(2).若在
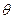 的取值范围内的任意
的取值范围内的任意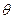 ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.(3).设x0>
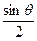 ,f(x0) >
,f(x0) >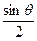 ,若f[f(x0)]=x0,求证f(x0)=x0
,若f[f(x0)]=x0,求证f(x0)=x0(1)
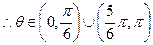
(2)
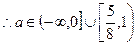
(3)略
解:(1)
令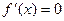 则
则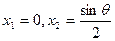
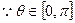
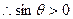
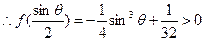

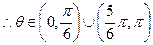 ----------------------------------(4分)
----------------------------------(4分)
(2)由(1)知 内为增函数
内为增函数
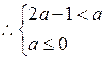 或
或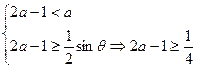
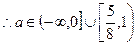 -----------------------------------(8分)
-----------------------------------(8分)
(3)证明:假设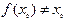 则
则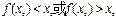
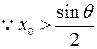 ,
, 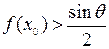
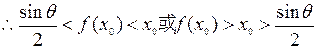
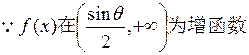
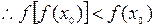 或
或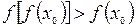
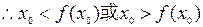 矛盾
矛盾
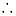 假设不成立
假设不成立 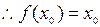 ---------------------------(12分)
---------------------------(12分)

令
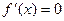 则
则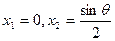
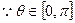
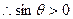
| x | 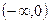 | 0 | 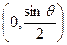 | 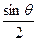 | 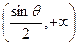 |
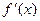 | + | 0 | _ | 0 | + |
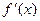 | 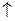 | 极大值 | 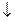 | 极小值 | 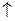 |
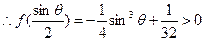

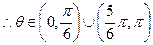 ----------------------------------(4分)
----------------------------------(4分)(2)由(1)知
 内为增函数
内为增函数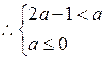 或
或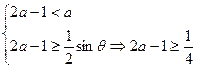
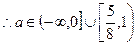 -----------------------------------(8分)
-----------------------------------(8分)(3)证明:假设
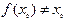 则
则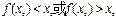
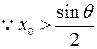 ,
, 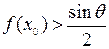
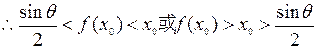
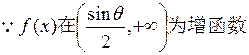
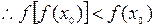 或
或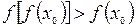
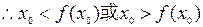 矛盾
矛盾 假设不成立
假设不成立 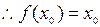 ---------------------------(12分)
---------------------------(12分)
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
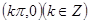 是正弦曲线的对称中心;(2)点
是正弦曲线的对称中心;(2)点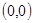 是余弦曲线的一个对称中心;(3)把余弦函数
是余弦曲线的一个对称中心;(3)把余弦函数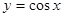 的图像向左平移
的图像向左平移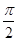 个单位,即得
个单位,即得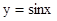 的图像;(4)在余弦曲线
的图像;(4)在余弦曲线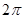 ;(5)在正弦曲线
;(5)在正弦曲线 中,相邻两个最高点的水平距离是
中,相邻两个最高点的水平距离是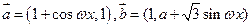 (
(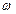 为常数且
为常数且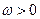 ),函数
),函数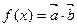 在
在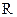 上的最大值为
上的最大值为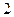 .(Ⅰ)求实数
.(Ⅰ)求实数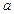 的值;(Ⅱ)把函数
的值;(Ⅱ)把函数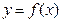 的图象向右平移
的图象向右平移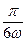 个单位,可得函数
个单位,可得函数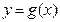 的图象,若
的图象,若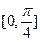 上为增函数,求
上为增函数,求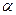 终边经过点P(-4,3),求
终边经过点P(-4,3),求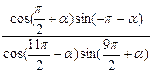 的值?
的值?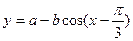 ,(b>0)在
,(b>0)在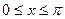 的最大值为
的最大值为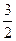 ,最小值为-
,最小值为-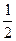 ,求2a+b的值?
,求2a+b的值?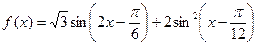 (
(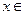 R).
R).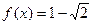 且
且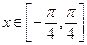 ,求x;(Ⅱ)求函数
,求x;(Ⅱ)求函数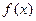 的单调递增区间.
的单调递增区间. .
. ,求
,求 的值;
的值; ,在△ABC中,角
,在△ABC中,角 的对边分别是
的对边分别是 且满足
且满足 ,求函数f(A)的取值范围.
,求函数f(A)的取值范围.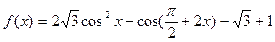
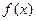 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;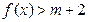 在
在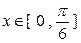 上恒成立,求实数
上恒成立,求实数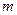 的取值范围.
的取值范围.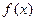 对任意
对任意 ,都有
,都有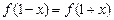 成立,设向量
成立,设向量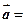 (sinx,2),
(sinx,2), (2sinx,
(2sinx, ),
),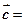 (cos2x,1),
(cos2x,1),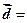 (1,2),当
(1,2),当 时,不等式f(
时,不等式f(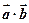 )>f(
)>f(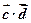 )的解集为
)的解集为 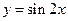 的图象向左平移
的图象向左平移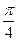 个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,则所得图象对应的函数解析式是 ( )
个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,则所得图象对应的函数解析式是 ( )