题目内容
(本小题满分12分)已知函数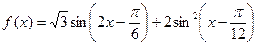 (
(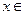 R).
R).
(Ⅰ)若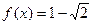 且
且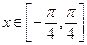 ,求x;(Ⅱ)求函数
,求x;(Ⅱ)求函数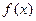 的单调递增区间.
的单调递增区间.
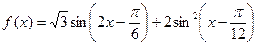 (
(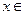 R).
R).(Ⅰ)若
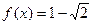 且
且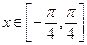 ,求x;(Ⅱ)求函数
,求x;(Ⅱ)求函数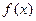 的单调递增区间.
的单调递增区间.(1)
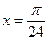
(2)

解:(Ⅰ)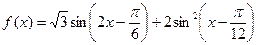
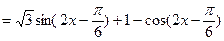
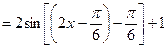
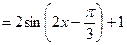 ----------------------------4分
----------------------------4分
因为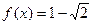 ,所以
,所以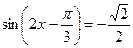 -----------------------------6分
-----------------------------6分
由于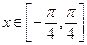 ,所以
,所以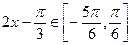 ,故
,故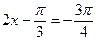 或
或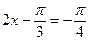
所以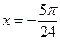 或
或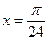 --------------------------------------------------------8分
--------------------------------------------------------8分
(Ⅱ)令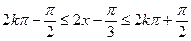 ------------------------------------------------10分
------------------------------------------------10分
解得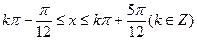
所以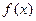 单调递增区间为
单调递增区间为 ---------------------12分
---------------------12分
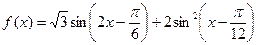
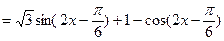
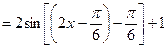
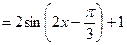 ----------------------------4分
----------------------------4分因为
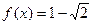 ,所以
,所以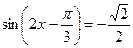 -----------------------------6分
-----------------------------6分由于
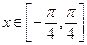 ,所以
,所以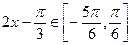 ,故
,故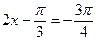 或
或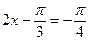
所以
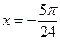 或
或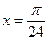 --------------------------------------------------------8分
--------------------------------------------------------8分(Ⅱ)令
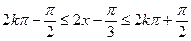 ------------------------------------------------10分
------------------------------------------------10分解得
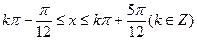
所以
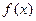 单调递增区间为
单调递增区间为 ---------------------12分
---------------------12分
练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 ,
,  .
. 的最大值和最小值;
的最大值和最小值; 上的图象与
上的图象与 轴的交点从左到右分别为M、N,图象的最高点为P,
轴的交点从左到右分别为M、N,图象的最高点为P,  与
与 的夹角的余弦.
的夹角的余弦.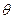 +
+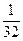 的极小值大于零,其中x∈R,
的极小值大于零,其中x∈R, 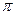 ].
].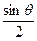 ,f(x0) >
,f(x0) >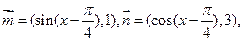
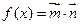 。
。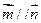 ,求
,求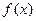 ;
;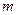 (
(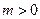 )个单位长度,再向下平移3个单位后图像对应的函数
)个单位长度,再向下平移3个单位后图像对应的函数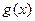 是奇函数,求
是奇函数,求
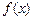 的最小正周期及
的最小正周期及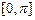 上的图象(在图上标明关键点的坐标)
上的图象(在图上标明关键点的坐标)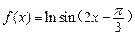 的单调递增区间是
的单调递增区间是 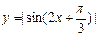 的最小正周期是
的最小正周期是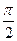 ;(2)函数
;(2)函数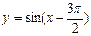 在区间
在区间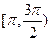 上单调递增;(3)
上单调递增;(3)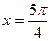 是函数
是函数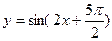 的图象的一
的图象的一 条对称轴.其中正确命题的个数是( )
条对称轴.其中正确命题的个数是( )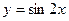 的图像经过怎样的平移变换得到函数
的图像经过怎样的平移变换得到函数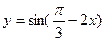 的图像 ( )
的图像 ( )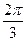 个单位长度
个单位长度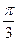 个单位长度
个单位长度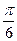 个单位长度
个单位长度