题目内容
【题目】已知椭圆![]() :
: ![]() (
(![]() )的上顶点到右顶点的距离为
)的上顶点到右顶点的距离为![]() ,左焦点为
,左焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程及
的标准方程及![]() 的取值范围;
的取值范围;
(Ⅱ)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() 恒为定值?若存在,求出点
恒为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(Ⅰ)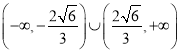 (Ⅱ)存在定点
(Ⅱ)存在定点![]() .
.
【解析】试题分析:(1)运用离心率公式和焦点坐标,直接求出a,b;
(2)利用设而不求的方法,表示出![]() ,设出要求的定值,利用对应项系数成比例明确出点
,设出要求的定值,利用对应项系数成比例明确出点![]() 的坐标
的坐标
试题解析:
(Ⅰ)由已知可得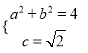 ,得
,得![]() ,
, ![]() ,
, ![]() .
.
过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() :
: ![]() .
.
由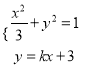 ,消去
,消去![]() 得
得![]() .
.
则![]()
![]() 或
或![]() ,
,
所以![]() 的取值范围是
的取值范围是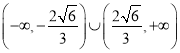
(Ⅱ)设![]() ,
, ![]() ,
,
则由(Ⅰ)知, ![]() ,
, ![]() .
.
又![]() ,
,
![]() .
.
假设存在点![]() ,则
,则![]() ,
, ![]() ,
,
所以![]()
![]()
![]() ,
,
要使得![]() (
(![]() 为常数),只要
为常数),只要![]() ,
,
从而![]() ,
,
整理得![]() ,解得
,解得![]() ,从而
,从而![]() ,
,
故存在定点![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.