题目内容
(2012•黄州区模拟)已知双曲线的顶点与焦点分别是椭圆
+
=1(a>b>0)的焦点与顶点,若双曲线的离心率为2,则椭圆离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
分析:先根据双曲线的顶点与焦点分别是椭圆的焦点与顶点,确定双曲线的顶点与焦点,由双曲线的离心率求出椭圆的离心率.
解答:解:由题意可设双曲线的方程为:
-
=1,(m>0,n>0)
∵椭圆
+
=1(a>b>0)的焦点(±c,0),顶点(±a,0),c2=a2-b2
由题意可得,双曲线的顶点为(±c,0),焦点为(±a,0)
∴m=c,n2+m2=a2
∵双曲线的离心率e=
=2
∴n=
m
∴b=n=
m,c=m,a=2m
椭圆的离心率e=
故选B
| x2 |
| m2 |
| y2 |
| n2 |
∵椭圆
| x2 |
| a2 |
| y2 |
| b2 |
由题意可得,双曲线的顶点为(±c,0),焦点为(±a,0)
∴m=c,n2+m2=a2
∵双曲线的离心率e=
| ||
| m |
∴n=
| 3 |
∴b=n=
| 3 |
椭圆的离心率e=
| 1 |
| 2 |
故选B
点评:本题以椭圆方程为载体,考查双曲线的几何性质,考查椭圆的离心率,正确运用几何量的关系是关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
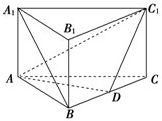 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为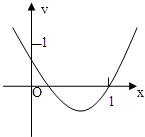 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )