题目内容
若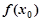 是函数
是函数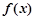 在点
在点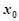 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称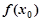 是函数
是函数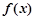 的一个极值,
的一个极值,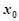 为极值点.已知
为极值点.已知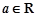 ,函数
,函数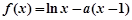 .
.
(Ⅰ)若 ,求函数
,求函数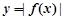 的极值点;
的极值点;
(Ⅱ)若不等式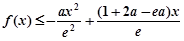 恒成立,求
恒成立,求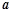 的取值范围.
的取值范围.
(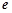 为自然对数的底数)
为自然对数的底数)
(1)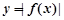 的极小值点为1和
的极小值点为1和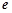 ,极大值点为
,极大值点为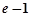 .
.
(2)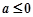
解析试题分析:解:(Ⅰ)若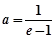 ,则
,则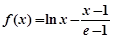 ,
,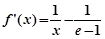 .
.
当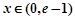 时,
时,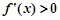 ,
,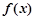 单调递增;
单调递增;
当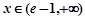 时,
时,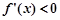 ,
,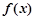 单调递减. …2分
单调递减. …2分
又因为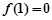 ,
,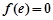 ,所以
,所以
当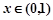 时,
时,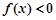 ;当
;当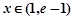 时,
时,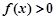 ;
;
当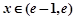 时,
时,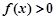 ;当
;当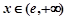 时,
时,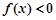 . …4分
. …4分
故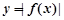 的极小值点为1和
的极小值点为1和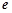 ,极大值点为
,极大值点为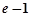 . …6分
. …6分
(Ⅱ)不等式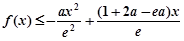 ,
,
整理为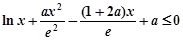 .…(*)
.…(*)
设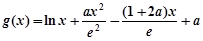 ,
,
则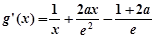 (
(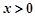 )
)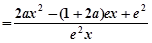
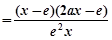 . …8分
. …8分
①当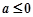 时,
时,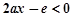 ,又
,又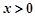 ,所以,
,所以,
当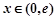 时,
时, ,
,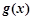 递增;
递增;
当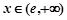 时,
时,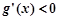 ,
,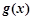 递减.
递减.
从而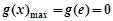 .
.
故,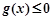 恒成立. …11分
恒成立. …11分
②当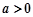 时,
时,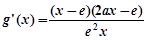
 .
.
令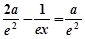 ,解得
,解得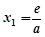 ,则当
,则当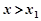 时,
时,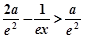 ;
;
再令 ,解得
,解得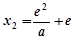 ,则当
,则当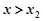 时,
时,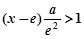 .
.
取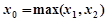 ,则当
,则当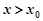 时,
时,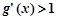 .
.
所以,当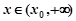 时,
时,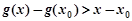 ,即
,即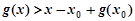 .
.
这与“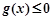 恒成立”矛盾.
恒成立”矛盾.
综上所述,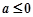 . …14分
. …14分
考点:导数的运用
点评:解决的关键是对于导数在研究函数中的运用,求解极值和最值,以及不等式的恒成立问题,属于基础题。

练习册系列答案
相关题目

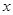 的不等式
的不等式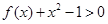
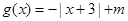 ,
,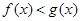 的解集非空,求实数m的取值范围
的解集非空,求实数m的取值范围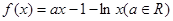
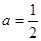 时,求函数在
时,求函数在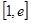 上的最大值和最小值;
上的最大值和最小值;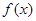 在
在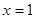 处取得极值,不等式
处取得极值,不等式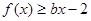 对
对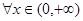 恒成立,求实数
恒成立,求实数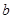 的取值范围。
的取值范围。 =
=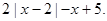
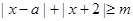 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.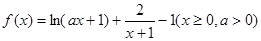 。
。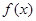 在
在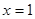 处取得极值,求
处取得极值,求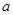 的值;
的值;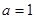 且
且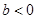 ,函数
,函数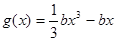 ,若对于
,若对于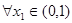 ,总存在
,总存在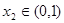 使得
使得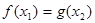 ,求实数
,求实数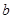 的取值范围。
的取值范围。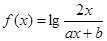 且
且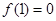 ,当
,当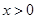 时,恒有
时,恒有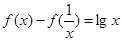
 的解析式;
的解析式;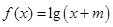 的解集为空集,求
的解集为空集,求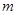 的范围。
的范围。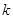 和
和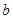 ,使得函数
,使得函数 和
和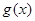 对其定义域上的任意实数
对其定义域上的任意实数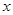 分别满足:
分别满足: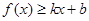 和
和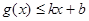 ,则称直线
,则称直线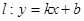 为
为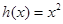 ,
,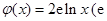 为自然对数的底数).
为自然对数的底数). 的极值;
的极值;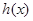 和
和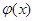 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由. 是R上的奇函数,且当
是R上的奇函数,且当 时,
时, ,求
,求 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;