题目内容
 (1)几何证明选讲:如图,CB是⊙O的直径,AP是⊙O的切线,A为切点,AP与CB的延长线交于点P,若PA=8,PB=4,求AC的长度.
(1)几何证明选讲:如图,CB是⊙O的直径,AP是⊙O的切线,A为切点,AP与CB的延长线交于点P,若PA=8,PB=4,求AC的长度.(2)坐标系与参数方程:在极坐标系Ox中,已知曲线C1:ρcos(θ+
| π |
| 4 |
| ||
| 2 |
(3)不等式选讲:解关于x的不等式|x-1|+a-2≤0(a∈R).
分析:(1)根据切割线定理,得PA2=PB×PC,结合PA=8、PB=4得PC=16=2PA.由△PAB∽△PCA,得AC=2AB,最后在Rt△ABC中利用勾股定理,算出AB=
,从而得到AC的长度是
;
(2)将曲线C1化成ρcosθ-ρsinθ=1,即直线x-y-1=0,再将曲线C2:ρ=1化成x2+y2=1,方程联解得A(1,0),B(0,-1).最后根据两点间的距离公式,算出|AB|=
,即得线段AB的长度;
(3)不等式|x-1|+a-2≤0即|x-1|≤2-a.然后分a=2、a>2和a<2三种情况加以讨论,分别解关于x的不等式|x-1|≤2-a,即可得到原不等式的解集.
| 12 |
| 5 |
| 5 |
| 24 |
| 5 |
| 5 |
(2)将曲线C1化成ρcosθ-ρsinθ=1,即直线x-y-1=0,再将曲线C2:ρ=1化成x2+y2=1,方程联解得A(1,0),B(0,-1).最后根据两点间的距离公式,算出|AB|=
| 2 |
(3)不等式|x-1|+a-2≤0即|x-1|≤2-a.然后分a=2、a>2和a<2三种情况加以讨论,分别解关于x的不等式|x-1|≤2-a,即可得到原不等式的解集.
解答:解:(1)∵AP是⊙O的切线,A为切点,∴PA2=PB×PC
∵PA=8,PB=4,∴PC=16,得PC=2PA
∵∠PAB=∠PCA,∠P是公共角
∴△PAB∽△PCA,得
=
=
,即AC=2AB
∵Rt△ABC中,BC=PC-PB=12
∴AC2+AB2=BC2,即5AB2=144,得AB=
∴AC=2AB=
,即AC的长度是
(2)曲线C1:ρcos(θ+
)=
,即ρ(cosθcos
-sinθsin
)=
∵cos
=sin
=
,
∴曲线C1化成ρcosθ-ρsinθ=1,即直线x-y-1=0,
将曲线C2:ρ=1化成普通方程,得x2+y2=1,原点为圆心、半径为1的圆
由
,解得A(1,0),B(0,-1)
∴|AB|=
=
,即线段AB的长度为
(3)不等式|x-1|+a-2≤0即|x-1|≤2-a
①当a=2时,不等式化成|x-1|≤0,解集为{1};
②当a>2时,因为2-a<0且|x-1|≥0,所以不等式的解集为∅;
③当a<2时,不等式|x-1|≤2-a化成a-2≤x-1≤2-a,得解集为{x|a-1≤x≤3-a}
∵PA=8,PB=4,∴PC=16,得PC=2PA
∵∠PAB=∠PCA,∠P是公共角
∴△PAB∽△PCA,得
| AB |
| AC |
| PA |
| PC |
| 1 |
| 2 |
∵Rt△ABC中,BC=PC-PB=12
∴AC2+AB2=BC2,即5AB2=144,得AB=
| 12 |
| 5 |
| 5 |
∴AC=2AB=
| 24 |
| 5 |
| 5 |
| 24 |
| 5 |
| 5 |
(2)曲线C1:ρcos(θ+
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∵cos
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴曲线C1化成ρcosθ-ρsinθ=1,即直线x-y-1=0,
将曲线C2:ρ=1化成普通方程,得x2+y2=1,原点为圆心、半径为1的圆
由
|
∴|AB|=
| (0-1)2+(-1-0)2 |
| 2 |
| 2 |
(3)不等式|x-1|+a-2≤0即|x-1|≤2-a
①当a=2时,不等式化成|x-1|≤0,解集为{1};
②当a>2时,因为2-a<0且|x-1|≥0,所以不等式的解集为∅;
③当a<2时,不等式|x-1|≤2-a化成a-2≤x-1≤2-a,得解集为{x|a-1≤x≤3-a}
点评:本题以圆中的比例线段、曲线的极坐标方程和含有绝对值的不等式解法为例,考查了切割线定理和相似三角形、极坐标与直角坐标的互化、直线与圆的位置关系和含有绝对值不等式解法等知识点,属于基础题.

练习册系列答案
相关题目
 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲如图,在正△ABC中,点D,E分别在边t上,且
选修4-1:几何证明选讲如图,在正△ABC中,点D,E分别在边t上,且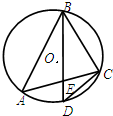 (2011•丹东模拟)选修4-1:几何证明选讲
(2011•丹东模拟)选修4-1:几何证明选讲 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤. 选修4-1:几何证明选讲
选修4-1:几何证明选讲