Question

【题目】已知椭圆 的右焦点为F（2，0），M为椭圆的上顶点，O为坐标原点，且△MOF是等腰直角三角形．
（1）求椭圆的方程；
（2）过点M分别作直线MA，MB交椭圆于A，B两点，设两直线的斜率分别为k1 ， k2 ， 且k1+k2=8，证明：直线AB过定点（ ）．

Answer 1

【答案】
（1）解：由△MOF是等腰直角三角形，得c2=b2=4，a2=8，

故椭圆方程为： =1．

（2）证明：

①若直线AB的斜率存在，设AB的方程为：y=kx+m，依题意得m≠±2，

设A（x1，y1），B（x2，y2），

由 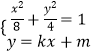，得（1+2k2）x2+4kmx+2m2﹣8=0，

则 ．

由已知 k1+k2=8，可得 ，

所以 ，即 ．

所以 ，整理得 ．

故直线AB的方程为 ，即y=k（ ）﹣2．

所以直线AB过定点（ ）．

②若直线AB的斜率不存在，设AB方程为x=x0，

设A（x0，y0），B（x0，﹣y0），

由已知 ，得 ．

此时AB方程为 ，显然过点（ ）．

综上，直线AB过定点（ ）．

【解析】（1）由△MOF是等腰直角三角形，得c2=b2=4，再根据a2=b2+c2可求得a；（2）分情况讨论：①当直线AB的斜率存在时，设AB的方程为：y=kx+m，联立直线AB方程与椭圆方程消掉y得x的二次方程，由韦达定理及k1+k2=8可得关于k，m的关系式，消m代入直线AB方程可求得定点坐标；②若直线AB的斜率不存在，设AB方程为x=x0 ， 由已知可求得AB方程，易验证其过定点；
【考点精析】掌握椭圆的标准方程是解答本题的根本，需要知道椭圆标准方程焦点在x轴：，焦点在y轴：．