Question

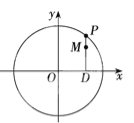
【题目】在平面直角坐标系中，圆O交x轴于点F1，F2，交y轴于点B1，B2．以B1，B2为顶点，F1，F2分别为左、右焦点的椭圆E，恰好经过点．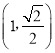

（1）求椭圆E的标准方程；

（2）设经过点（﹣2，0）的直线l与椭圆E交于M，N两点，求△F2MN面积的最大值．

Answer 1

【答案】（1）．（2）最大值．

【解析】

(1)根据题意分析椭圆中基本量的关系,再代入求解即可.

(2)设直线,再联立直线与椭圆的方程,代入韦达定理求得弦长的解析式,再求解到的距离,进而表达出面积的表达式,换元后利用二次不等式的方法求最值即可.

（1）由已知可得,椭圆E的焦点在x轴上.

设椭圆E的标准方程为,焦距为2c,则b＝c,

∴a2＝b2+c2＝2b2,∴椭圆E的标准方程为.

又椭圆E过点,∴,解得b2＝1.

∴椭圆E的标准方程为.

（2）由于点（﹣2,0）在椭圆E外,所以直线l的斜率存在.

设直线l的斜率为k,则直线l：y＝k（x+2）,设M（x1,y1）,N（x2,y2）.

由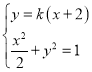消去y得,（1+2k2）x2+8k2x+8k2﹣2＝0.

由△＞0得,从而,

∴.

∵点F2（1,0）到直线l的距离,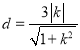

∴△F2MN的面积为.

令1+2k2＝t,则t∈[1,2）,

∴,

当即时,S有最大值,,此时.

所以,当直线l的斜率为时,可使△F2MN的面积最大,其最大值.