题目内容
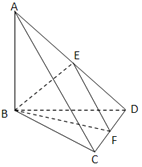
【题目】已知四面体ABCD中AB⊥面BCD，BC⊥DC，BE⊥AD垂足为E，F为CD中点，AB＝BD＝2，CD＝1．
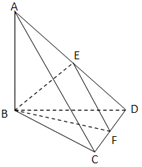
（1）求证：AC∥面BEF；
（2）求点B到面ACD的距离．
【答案】（1）见解析；（2）
.
【解析】
（1）先证得
，然后利用直线与平面平行的判定定理，即可证得AC∥面BEF；
（2）设点
到平面
的距离为
，利用
，即可求得点B到面ACD的距离．
（1）因为BE⊥AD，AB＝BD，所以E为AD中点，
又因为F是CD中点，所以AC∥EF，
而AC
面BEF，EF面BEF，所以AC∥面BEF.
（2）由已知，可得BC
，AD
，AC
，
，
因为
，所以
为直角三角形其面积
，
又由BC⊥DC，且
，所以
,
BCD的面积
，
设点B到面ACD的距离为h，
因为VA﹣BCD＝VB﹣ACD，即
，解得
，
所以点B到面ACD的距离为
．
星级口算天天练系列答案【题目】孝感市某中学为了解中学生的课外阅读时间，决定在该中学的1200名男生和800名女生中用分层抽样的方法抽取20名学生，对他们的课外阅读时间进行问卷调查.现在按课外阅读时间的情况将学生分成三类：
类（不参加课外阅读），
类（参加课外阅读，但平均每周参加课外阅读的时间不超过3小时），
类（参加课外阅读，且平均每周参加课外阅读的时间超过3小时）.调查结果如表：
|
|
| |
男生 |
| 5 | 3 |
女生 |
| 3 | 3 |
（1）求出表中
的值；
（2）根据表中的统计数据，完成下面的列联表，井判断是否有90%的把握认为“参加阅读与否”与性别有关；
男生 | 女生 | 总计 | |
不参加课外阅读 | |||
参课外阅读 | |||
总计 |
（3）从抽出的女生中再随机抽取3人进一步了解情况，记X为抽取的这3名女生中A类女生人数，求X的数学期望.
附:
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
【题目】某商店为了更好地规划某种商品进货的量，该商店从某一年的销售数据中，随机抽取了
组数据作为研究对象，如下表所示（
（吨）为该商品进货量，
（天）为销售天数）：
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（Ⅰ）根据上表提供的数据，求出关于的线性回归方程
；
（Ⅱ）在该商品进货量（吨）不超过
（吨）的前提下任取两个值，求该商品进货量（吨）恰有一个值不超过
（吨）的概率.
参考公式和数据：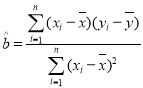
，
.
，
.
