题目内容
(Ⅰ) 复数z满足(1+2i)z+(3-10i)
=4-34i,求z;
(Ⅱ) 已知z=1+i,设z,z2,z-z2在复平面对应的点分别为A,B,C,求△ABC的面积.
. | z |
(Ⅱ) 已知z=1+i,设z,z2,z-z2在复平面对应的点分别为A,B,C,求△ABC的面积.
分析:(Ⅰ)利用复数的运算性质即可得出;
(Ⅱ)利用复数的运算性质及复数的几何意义即可算出.
(Ⅱ)利用复数的运算性质及复数的几何意义即可算出.
解答:解:(Ⅰ)∵(1+2i)z+(3-10i)
=4-34i,
∴(4-8i)z=4-34i,即(2-4i)z=2-17i,
∴(2-4i)(2+4i)z=(2-17i)(2+4i),化为20z=72-26i,
∴z=
-
i.
(Ⅱ)∵z=1+i,∴z2=(1+i)2=2i,z-z2=(1+i)-2i=1-i.如图所示: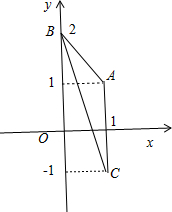
∵1+i与1-i关于x轴对称,∴AC⊥x轴,且
=(1,1)-(1,-1)=(0,2),
∴|
|=
=2,
∵AC⊥x轴,∴点B到AC的距离为1.
∴S△ABC=
×2×1=1
. |
| z |
∴(4-8i)z=4-34i,即(2-4i)z=2-17i,
∴(2-4i)(2+4i)z=(2-17i)(2+4i),化为20z=72-26i,
∴z=
| 18 |
| 5 |
| 13 |
| 10 |
(Ⅱ)∵z=1+i,∴z2=(1+i)2=2i,z-z2=(1+i)-2i=1-i.如图所示:

∵1+i与1-i关于x轴对称,∴AC⊥x轴,且
| CA |
∴|
| CA |
| 02+22 |
∵AC⊥x轴,∴点B到AC的距离为1.
∴S△ABC=
| 1 |
| 2 |
点评:熟练掌握复数的运算性质和几何意义是解题的关键.

练习册系列答案
相关题目
如果复数Z满足|Z+i|+|Z-i|=2,那么|Z+i+1|最小值是( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|