题目内容
11.函数y=sinxcosx+$\sqrt{3}$cos2x-$\sqrt{3}$的图象的对称中心是($\frac{1}{2}$kπ-$\frac{π}{6}$,-$\frac{\sqrt{3}}{2}$),(k∈Z).分析 首先,化简函数解析式,然后,结合三角函数的对称性求解即可.
解答 解:y=sinxcosx+$\sqrt{3}$cos2x-$\sqrt{3}$
=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}(1+cos2x)$-$\sqrt{3}$,
=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x-$\frac{\sqrt{3}}{2}$
=sin(2x+$\frac{π}{3}$)-$\frac{\sqrt{3}}{2}$,
∴f(x)=sin(2x+$\frac{π}{3}$)-$\frac{\sqrt{3}}{2}$,
∴2x+$\frac{π}{3}$=kπ,
∴x=$\frac{1}{2}$kπ-$\frac{π}{6}$,k∈Z,
∴对称中心为($\frac{1}{2}$kπ-$\frac{π}{6}$,-$\frac{\sqrt{3}}{2}$),(k∈Z).
故答案为:($\frac{1}{2}$kπ-$\frac{π}{6}$,-$\frac{\sqrt{3}}{2}$),(k∈Z).
点评 本题重点考查了三角函数的图象与性质,属于中档题.

练习册系列答案
相关题目
1.“点P在平面α内,直线l与平面α相交于点Q”可以用符号表示为( )
| A. | P?α,l∩α=Q | B. | P∈α,l∪α=Q | C. | P∈α,l∩α=Q | D. | P?α,l∪α=Q |
2.已知函数f(x)=sinx,下列式子中成立的是( )
| A. | f(x+π)=sinx | B. | f(2π-x)=sinx | C. | f(x-$\frac{π}{2}$)=-cosx | D. | f(π-x)=-f(x) |
6.设a是空间中的一条直线,α是空间中的一个平面,则下列说法正确的是( )
| A. | 过a一定存在平面β,使得β∥α | |
| B. | 过a一定存在平面β,使得β⊥α | |
| C. | 在平面α内一定不存在直线b,使得a⊥b | |
| D. | 在平面α内一定不存在直线b,使得a∥b |
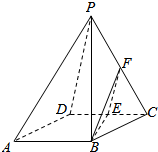 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.