题目内容
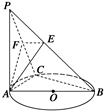
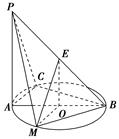
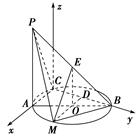
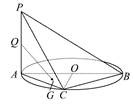
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.
(1)求证:平面MOE∥平面PAC.
(2)求证:平面PAC⊥平面PCB.
(3)设二面角M—BP—C的大小为θ,求cos θ的值.

(1)求证:平面MOE∥平面PAC.
(2)求证:平面PAC⊥平面PCB.
(3)设二面角M—BP—C的大小为θ,求cos θ的值.
(1)见解析 (2)见解析 (3)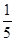
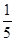
(1)因为点E为线段PB的中点,点O为线段AB的中点,所以OE∥PA.
因为PA?平面PAC,OE?平面PAC,
所以OE∥平面PAC.
因为OM∥AC,
因为AC?平面PAC,OM?平面PAC,
所以OM∥平面PAC.
因为OE?平面MOE,OM?平面MOE,OE∩OM=O,
所以平面MOE∥平面PAC.
(2)因为点C在以AB为直径的⊙O上,
所以∠ACB=90°,即BC⊥AC.
因为PA⊥平面BAC,BC?平面ABC,
所以PA⊥BC.
因为AC?平面PAC,PA?平面PAC,PA∩AC=A,
所以BC⊥平面PAC.
因为BC?平面PCB,
所以平面PAC⊥平面PCB.
(3)如图,以C为原点,CA所在的直线为x轴,CB所在的直线为y轴,建立空间直角坐标系C—xyz.
因为∠CBA=30°,PA=AB=2,
所以CB=2cos 30°= ,AC=1.
,AC=1.
延长MO交CB于点D.
因为OM∥AC,
所以MD⊥CB,MD=1+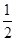 =
=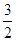 ,
,
CD=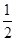 CB=
CB=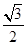 .
.
所以P(1,0,2),C(0,0,0),B(0, ,0),M
,0),M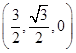 .
.
所以 =(1,0,2),
=(1,0,2), =(0,
=(0, ,0).
,0).
设平面PCB的法向量m=(x,y,z).
因为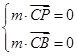
所以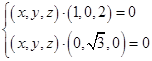 ,即
,即
令z=1,则x=-2,y=0.
所以m=(-2,0,1).
同理可求平面PMB的一个法向量n=(1, ,1).
,1).
所以cos〈m,n〉=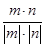 =-
=-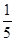 .
.
因为二面角M—BP—C为锐二面角,所以cos θ=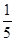 .
.
因为PA?平面PAC,OE?平面PAC,
所以OE∥平面PAC.
因为OM∥AC,
因为AC?平面PAC,OM?平面PAC,
所以OM∥平面PAC.
因为OE?平面MOE,OM?平面MOE,OE∩OM=O,
所以平面MOE∥平面PAC.
(2)因为点C在以AB为直径的⊙O上,
所以∠ACB=90°,即BC⊥AC.
因为PA⊥平面BAC,BC?平面ABC,
所以PA⊥BC.
因为AC?平面PAC,PA?平面PAC,PA∩AC=A,
所以BC⊥平面PAC.
因为BC?平面PCB,
所以平面PAC⊥平面PCB.
(3)如图,以C为原点,CA所在的直线为x轴,CB所在的直线为y轴,建立空间直角坐标系C—xyz.

因为∠CBA=30°,PA=AB=2,
所以CB=2cos 30°=
 ,AC=1.
,AC=1.延长MO交CB于点D.
因为OM∥AC,
所以MD⊥CB,MD=1+
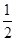 =
=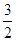 ,
,CD=
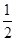 CB=
CB=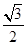 .
.所以P(1,0,2),C(0,0,0),B(0,
 ,0),M
,0),M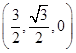 .
.所以
 =(1,0,2),
=(1,0,2), =(0,
=(0, ,0).
,0).设平面PCB的法向量m=(x,y,z).
因为
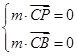
所以
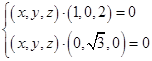 ,即
,即
令z=1,则x=-2,y=0.
所以m=(-2,0,1).
同理可求平面PMB的一个法向量n=(1,
 ,1).
,1).所以cos〈m,n〉=
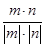 =-
=-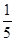 .
.因为二面角M—BP—C为锐二面角,所以cos θ=
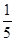 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
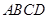 为正方形,
为正方形,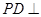 平面
平面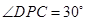 ,
,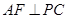 于点
于点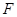 ,
,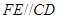 ,交
,交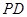 于点
于点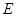 .
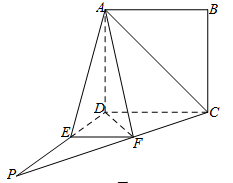
.
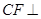 平面
平面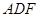 ;
;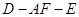 的余弦值.
的余弦值.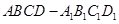 中,底面ABCD和侧面
中,底面ABCD和侧面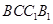 都是矩形,E是CD的中点,
都是矩形,E是CD的中点,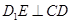 ,
,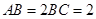 .
.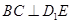 ;
;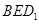 所成的锐二面角的大小为
所成的锐二面角的大小为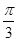 ,求线段
,求线段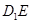 的长度.
的长度.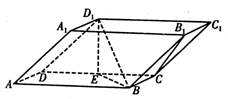
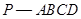 中,
中,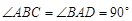 ,
,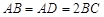 ,
,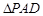 为正三角形,且平面
为正三角形,且平面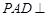 平面
平面 .
.
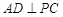 ;
;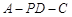 的余弦值.
的余弦值.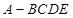 ,
,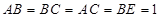 ,
,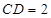 ,
,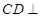 平面
平面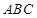 ,
,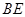 ∥
∥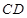 ,
,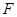 为
为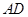 的中点.
的中点.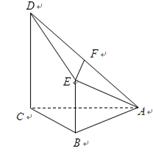
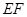 ∥平面
∥平面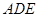
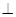 平面
平面 ;
;