题目内容
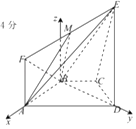
【题目】如图所示,等腰梯形ABCD的底角A等于60°.直角梯形ADEF所在的平面垂直于平面 ABCD,∠EDA=90°,且ED=AD=2AF=2AB=2.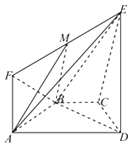
(Ⅰ)证明:平面ABE⊥平面EBD;
(Ⅱ)点M在线段EF上,试确定点M的位置,使平面MAB与平面ECD所成的角的余弦值为 ![]() .
.
【答案】(I)证明:∵平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD,ED⊥AD,ED平面ADEF, ∴ED⊥平面ABCD,∵AB平面ABCD,
∴ED⊥AD,
∵AB=1,AD=2,∠BAD=60°,
∴BD= ![]() =
= ![]() ,
,
∴AB2+BD2=AD2 , ∴AB⊥BD,
又BD平面BDE,ED平面BDE,BD∩ED=D,
∴AB⊥平面BDE,又AB平面ABE,
∴平面ABE⊥平面EBD.
(II)解:以B为原点,以BA,BD为x轴,y轴建立空间直角坐标系B﹣xyz,
则A(1,0,0),B(0,0,0),C(﹣ ![]() ,
, ![]() ,0),D(0,
,0),D(0, ![]() ,0),E(0,
,0),E(0, ![]() ,2),
,2),
F(1,0,1),则 ![]() =(
=( ![]() ,
, ![]() ,0),
,0), ![]() =(0,0,2),
=(0,0,2), ![]() =(1,0,0),
=(1,0,0), ![]() =(1,﹣
=(1,﹣ ![]() ,﹣1),
,﹣1),
设 ![]() =λ
=λ ![]() =(λ,﹣
=(λ,﹣ ![]() λ,﹣λ)(0≤λ≤1),则
λ,﹣λ)(0≤λ≤1),则 ![]() =
= ![]() +
+ ![]() =(λ,
=(λ, ![]() ﹣
﹣ ![]() ,2﹣λ),
,2﹣λ),
设平面CDE的法向量为 ![]() =(x1 , y1 , z1),平面ABM的法向量为
=(x1 , y1 , z1),平面ABM的法向量为 ![]() =(x2 , y2 , z2),
=(x2 , y2 , z2),
则 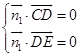 ,
, 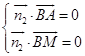 ,
,
∴ 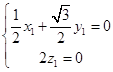 ,
,  ,
,
令y1=1得 ![]() =(﹣
=(﹣ ![]() ,1,0),令y2=2﹣λ得
,1,0),令y2=2﹣λ得 ![]() =(0,2﹣λ,
=(0,2﹣λ, ![]() ),
),
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,解得λ=
,解得λ= ![]() ,
,
∴当M为EF的中点时,平面MAB与平面ECD所成的角的余弦值为 ![]() .
.
【解析】(I)计算BD,根据勾股定理逆定理得出AB⊥BD,再根据ED⊥平面ABCD得出ED⊥AB,故而AB⊥平面ADEF,从而平面ABE⊥平面EBD;(II)建立空间坐标系,设 ![]() =λ
=λ ![]() ,求出两平面的法向量,令法向量的夹角余弦值的绝对值等于
,求出两平面的法向量,令法向量的夹角余弦值的绝对值等于 ![]() ,解出λ即可得出结论.
,解出λ即可得出结论.
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直).

【题目】某市食品药品监督管理局开展2019年春季校园餐饮安全检查,对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如下表所示:
中学编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
卫生标准评分y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;(精确到0.1)
(2)现从8个被检查的中学食堂中任意抽取两个组成一组,若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分,则组成“对比标兵食堂”,求该组被评为“对比标兵食堂”的概率.
参考公式: ,
,![]() ;
;
参考数据:![]() ,
,![]() .
.
【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响,部分统计数据如下:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 |
|
| |
学习成绩不优秀 |
|
| |
合计 |
(1)根据以上统计数据,你是否有![]() 的把握认为使用智能手机对学习有影响?
的把握认为使用智能手机对学习有影响?
(2)为了进一步了解学生对智能手机的使用习惯,现在对以上使用智能手机的高中时采用分层抽样的方式,抽取一个容量为![]() 的样本,若抽到的学生中成绩不优秀的比成绩优秀的多
的样本,若抽到的学生中成绩不优秀的比成绩优秀的多![]() 人,求
人,求![]() 的值.
的值.
|
|
|
|
|
|
|
|
|
|
|
|
![]()