题目内容
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式,并用定义法证明
的解析式,并用定义法证明![]() 在
在![]() 单调递增;
单调递增;
(3)已知![]() ,设P:
,设P:![]() ,不等式
,不等式![]() 恒成立,Q:
恒成立,Q:![]() 时,
时,![]() 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的![]() 的集合记为A,满足Q成立的
的集合记为A,满足Q成立的![]() 集合记为B,求
集合记为B,求![]() (R为全集)。
(R为全集)。
【答案】(1)![]() (2)
(2)![]() ,证明见解析(3)
,证明见解析(3)![]()
【解析】
(1)令![]() ,由条件,结合f(1)=0,即可得到f(0);
,由条件,结合f(1)=0,即可得到f(0);
(2)令y=0,结合f(0),即可求出f(x)的解析式,利用定义证明函数的单调性;
(3)化简不等式f(x)+3<2x+a,得到x2﹣x+1<a,求出左边的范围,由恒成立得到a的范围;由二次函数的单调性,即可得到集合B,从而求出A∩RB.
解:(1)令![]() 则有
则有![]() ,又
,又![]()
(2)令![]() 又
又![]() ,
,![]() ;
;
任取![]() ,
,![]()
由![]() ,
,![]() ,则
,则![]() 在
在![]() 单调递增。
单调递增。
(3)由P成立得![]() 当
当![]() 时,
时,![]()
![]()
由![]() 在
在![]() 是单调函数,
是单调函数,![]() ,
,
得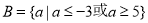 ,
,![]() 。
。

练习册系列答案
相关题目