题目内容
若函数
 在区间
在区间 ,0)内单调递增,则
,0)内单调递增,则 的取值范围
的取值范围
是( )

 在区间
在区间 ,0)内单调递增,则
,0)内单调递增,则 的取值范围
的取值范围 是( )
A.[ ,1) ,1) | B.[ ,1) ,1) | C.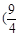 , , | D.(1, ) ) |
B
分析:将函数看作是复合函数,令g(x)=x3-ax,且g(x)>0,得x∈(-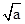 ,0)∪(
,0)∪(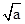 ,+∞),因为函数是高次函数,所以用导数来判断其单调性,再由复合函数“同增异减”求得结果.
,+∞),因为函数是高次函数,所以用导数来判断其单调性,再由复合函数“同增异减”求得结果.
解答:解:设g(x)=x3-ax,g(x)>0,得x∈(-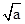 ,0)∪(
,0)∪(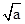 ,+∞),?
,+∞),?
g′(x)=3x2-a,x∈(- ,
, )时,g(x)递减,?
)时,g(x)递减,?
x∈(-∞,- )或x∈(
)或x∈( ,+∞)时,g(x)递增.?
,+∞)时,g(x)递增.?
∴当a>1时,减区间为(- ,0),?不合题意,
,0),?不合题意,
当0<a<1时,(- ,0)为增区间.?
,0)为增区间.?
∴(- ,0)∩(-
,0)∩(- ,0).?
,0).?
∴a∈[ ,1)
,1)
故选B.
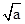 ,0)∪(
,0)∪(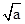 ,+∞),因为函数是高次函数,所以用导数来判断其单调性,再由复合函数“同增异减”求得结果.
,+∞),因为函数是高次函数,所以用导数来判断其单调性,再由复合函数“同增异减”求得结果.解答:解:设g(x)=x3-ax,g(x)>0,得x∈(-
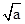 ,0)∪(
,0)∪(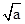 ,+∞),?
,+∞),?g′(x)=3x2-a,x∈(-
 ,
, )时,g(x)递减,?
)时,g(x)递减,?x∈(-∞,-
 )或x∈(
)或x∈( ,+∞)时,g(x)递增.?
,+∞)时,g(x)递增.?∴当a>1时,减区间为(-
 ,0),?不合题意,
,0),?不合题意,当0<a<1时,(-
 ,0)为增区间.?
,0)为增区间.?∴(-
 ,0)∩(-
,0)∩(- ,0).?
,0).?∴a∈[
 ,1)
,1)故选B.

练习册系列答案
相关题目
 的图象恒过定点
的图象恒过定点 ,若点
,若点 上,其中
上,其中 ,则
,则 的最小值为_______.
的最小值为_______. 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且 上的最大值是12.
上的最大值是12. 使得方程
使得方程 在区间
在区间 内有且只有两个不等的实
内有且只有两个不等的实 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. 在
在 上的单调性,并证明之.
上的单调性,并证明之. 满足
满足 (
( 是虚数单位),则复数
是虚数单位),则复数



 的方程
的方程 有一个正根和一个负根,则
有一个正根和一个负根,则 的取值范围是
的取值范围是
 ,若
,若 ,则
,则 的取值范围是 .
的取值范围是 . ,则
,则
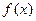 是一次函数,
是一次函数,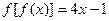 且,则
且,则