题目内容
已知定点A（0，7）、B（0，-7）、C（12，2），以C为一个焦点作过A、B的椭圆，求另一焦点F的轨迹方程.
点F的轨迹方程是y2-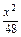
=1(y≤-1)
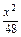=1(y≤-1) 设F（x，y）为轨迹上的任意一点，
∵A、B两点在以C、F为焦点的椭圆上，
∴|FA|+|CA|=2a，|FB|+|CB|=2a（其中a表示椭圆的长半轴长），
∴|FA|+|CA|=|FB|+|CB|，
∴|FA|-|FB|=|CB|-|CA|
=
-
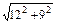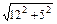=2.
∴|FA|-|FB|=2.
由双曲线的定义知，F点在以A、B为焦点，2为实轴长的双曲线的下半支上，
∴点F的轨迹方程是y2-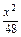=1(y≤-1).
∵A、B两点在以C、F为焦点的椭圆上，
∴|FA|+|CA|=2a，|FB|+|CB|=2a（其中a表示椭圆的长半轴长），
∴|FA|+|CA|=|FB|+|CB|，
∴|FA|-|FB|=|CB|-|CA|
=
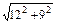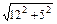-=2.∴|FA|-|FB|=2.
由双曲线的定义知，F点在以A、B为焦点，2为实轴长的双曲线的下半支上，
∴点F的轨迹方程是y2-
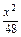=1(y≤-1).
练习册系列答案
相关题目
=
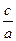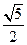,且双曲线与椭圆4x2+9y2=36有公共焦点，则双曲线的方程是( )
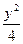-x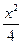2="1"
-y2=1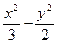
=1上截得弦长为4,其斜率为2,则直线l在y轴上的截距是_____________.
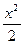－y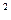
=1有公共渐近线的双曲线方程是（ ）
－
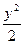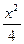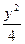="1"
=1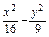
=1共渐近线，且过点A（2
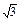，-3）的双曲线方程.
－
=1的两焦点为F1、F2，点P在双曲线上，且直线PF1、PF2倾斜角之差为
,则△PF1F2的面积为
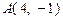和双曲线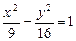
右焦点的直线方程为 .