题目内容
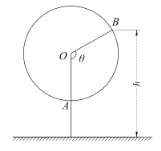
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(Ⅰ)若![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段的长度;
截得的线段的长度;
(Ⅱ)若![]() ,在曲线
,在曲线![]() 上求一点
上求一点![]() ,使得点
,使得点![]() 到直线
到直线![]() 的距离最小,并求出最小距离.
的距离最小,并求出最小距离.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ)由题意,得曲线![]() 的普通方程和直线
的普通方程和直线![]() 的普通方程,联立方程组,解焦点,即可求解截曲线
的普通方程,联立方程组,解焦点,即可求解截曲线![]() 的线段长;
的线段长;
(Ⅱ)解法一:![]() 时,得直线
时,得直线![]() 的普通方程,由点到直线的距离公式,得到距离的表达式,转化为三角函数的性质,即可求解最小值.
的普通方程,由点到直线的距离公式,得到距离的表达式,转化为三角函数的性质,即可求解最小值.
试题解析:
(Ⅰ)曲线![]() 的普通方程为
的普通方程为![]() .
.
当![]() 时,直线
时,直线![]() 的普通方程为
的普通方程为![]() .
.
由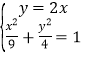 .解得
.解得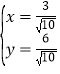 或
或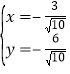 ,
,
直线![]() 被曲线
被曲线![]() 截得的线段的长度为
截得的线段的长度为![]() .
.
(Ⅱ)解法一:![]() 时,直线
时,直线![]() 的普通方程为
的普通方程为![]() .
.
由点到直线的距离公式,椭圆![]() 上的点
上的点![]() 到直线
到直线![]() :
:![]() 的距离为
的距离为
![]()
![]()
![]() ,
,
其中![]() 满足
满足![]() ,
,![]() .
.
由三角函数性质知,当![]() 时,
时,![]() 取最小值
取最小值![]() .
.
此时,![]() ,
,![]() .
.
因此,当点![]() 位于
位于![]() 时,点
时,点![]() 到
到![]() 的距离取最小值
的距离取最小值![]() .
.
解法二:当![]() 时,直线
时,直线![]() 的普通方程为
的普通方程为![]() .
.
设与![]() 平行,且与椭圆
平行,且与椭圆![]() 相切的直线
相切的直线![]() 的方程为
的方程为![]() .
.
由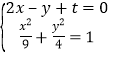 消去
消去![]() 并整理得
并整理得![]() .
.
由判别式![]() ,解得
,解得![]() .
.
所以,直线![]() 的方程为
的方程为![]() ,或
,或![]() .
.
要使两平行直线![]() 与
与![]() 间的距离最小,则直线
间的距离最小,则直线![]() 的方程为
的方程为![]() .
.
这时,![]() 与
与![]() 间的距离
间的距离![]()
![]() .
.
此时点![]() 的坐标为方程组
的坐标为方程组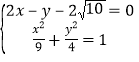 的解
的解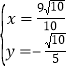 .
.
因此,当点![]() 位于
位于![]() 时,点
时,点![]() 到直线
到直线![]() 的距离取最小值
的距离取最小值![]() .
.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() =bx+a;(其中
=bx+a;(其中 ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
【题目】交通安全法有规定:机动车行经人行横道时,应当减速行驶;遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇行人横过马路,应当避让.我们将符合这条规定的称为“礼让斑马线”,不符合这条规定的称为“不礼让斑马线”.下表是六安市某十字路口监控设备所抓拍的5个月内驾驶员“不礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
“不礼让斑马线”的驾驶员人数 | 120 | 105 | 100 | 85 | 90 |
(1)根据表中所给的5个月的数据,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求“不礼让斑马线”的驾驶员人数![]() 关于月份
关于月份![]() 之间的线性回归方程;
之间的线性回归方程;
(3)若从4,5月份“不礼让斑马线”的驾驶员中分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的2人分别来自两个月份的概率;
参考公式:线性回归方程![]() ,其中
,其中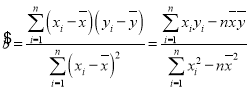 ,
,![]() ,
, .
.