题目内容
【题目】在线段
的两端点各置一个光源，已知光源
，
的发光强度之比为
，则线段上光照度最小的一点到，的距离之比为______（光学定律：
点的光照度与到光源的距离的平方成反比，与光源的发光强度成正比）
【答案】
【解析】
设线段长为L，线段上光照度最小的一点P到
，
的距离分别为
，不妨设，光源的发光强度之比为1，2，由题意可得P点受光源的照度为：
，P点受光源的照度为：
，作和后利用导数求最值，可得P到，的距离，作比得答案．
解：设线段长为L，线段上光照度最小的一点P到，的距离分别为，不妨设，光源的发光强度为1，2，
∵光照度与光的强度成正比，设比例系数为
，
与光源距离的平方成反比，设比例系数为
，
故P点受光源的照度为：，
P点受光源的照度为：，
故P点受到，两光源的总照度
，
，
令
，解得：
，
当
时，
，函数
在
上递减，
当
时，
，函数在
上递增，
故当时，
取极小值，且是最小值，
故P在线段上距离为
时，P点的光照度最小，
此时点P到的距离，之比为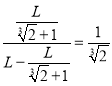
．
故答案为：.
练习册系列答案
相关题目
