题目内容
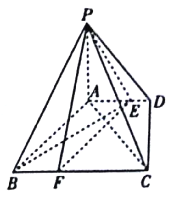
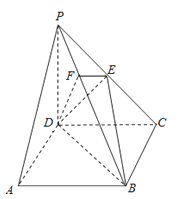
【题目】如图为一简单组合体，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC=2．
（1）请画出该几何体的三视图；
（2）求四棱锥B﹣CEPD的体积．
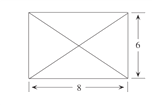
【答案】解：（1）该组合体的主视图和侧视图如图示：
（2）∵PD平面ABCD，PD平面PDCE
∴平面PDCE⊥平面ABCD
∵BC⊥CD
∴BC⊥平面PDCE（5分）
∵SPCDE=
（PD+EC）DC=3
∴四棱锥B﹣CEPD的体积
V=
SPCDEBC=2．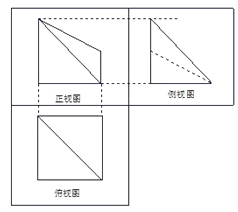
【解析】（1）由已知中底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC=2．根据三视图的定义，易得到该几何体的三视图；
（2）由已知中PD⊥平面ABCD，且PD=AD=2EC=2，我们计算出棱锥的底面面积和高，代入棱体积公式，即可求出四棱锥B﹣CEPD的体积；
【考点精析】本题主要考查了简单空间图形的三视图的相关知识点，需要掌握画三视图的原则：长对齐、高对齐、宽相等才能正确解答此题．
练习册系列答案
相关题目
