题目内容
【题目】已知函数
．
（1）求函数
的图象在
处的切线方程；
（2）若任意
，不等式
恒成立，求实数
的取值范围；
（3）设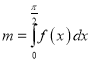
， 
，证明： 
．
【答案】（1）
（2） 
（3）见解析
【解析】试题分析：（1）本问考查导数的几何意义， 
， 
，于是可得切线方程为
；（2）本问考查利用导数研究恒成立问题，不等式
恒成立
，设函数
，则转化为当
时， 
恒成立，对函数
求导， 
，再令
，对
求导， 
，通过对
分区间讨论，使得
恒成立，从而得到
的取值范围；（3）首先通过微积分定理求出
，则
，由（2）知，当
时， 
，即
，构造函数
，通过证明该函数的单调性，易得出
在
上恒成立，令
，于是通过不等式的放缩，可以得到待证明的结论.
试题解析：（1）
， 
，∴切线为
（2）
，令
则
又令
①当
，即
时， 
恒成立，∴
递增
∴
，∴
，∴
递增
∴
（不合题意）
②当
即
时， 
递减，
∴
，∴
，∴
递减
∴
（符合题意）
③当
，即
时，由
，∴在
上， 
，使
且
时， 
，∴
递增，∴
（不符合题意）
综上： 
.
（3）
∴
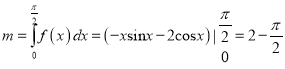
，由（2）知，当
时， 
，∴
，
又令
， 
，∴
递减
即
在
上恒成立，令
∴原不等式
∴左式
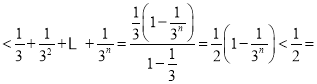右式
∴得证.
【题目】（本小题满分12分） 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表（假设该区域空气质量指数不会超过
）：
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在
年
天的空气质量指数监测数据作为样本，绘制的频率分布直方图如下图，把该直方图所得频率估计为概率．
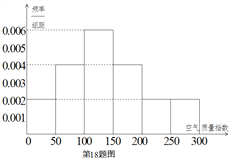
（Ⅰ）请估算
年（以
天计算）全年空气质量优良的天数(未满一天按一天计算)；
（Ⅱ）该校
年
月
、
日将作为高考考场，若这两天中某天出现
级重度污染，需要净化空气费用
元，出现
级严重污染，需要净化空气费用
元，记这两天净化空气总费用为
元，求
的分布列及数学期望．
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一个周期内的图象时，列表并填入的部分数据如表：
x |
|
| |||
ωx+φ | 0 |
| π |
| 2π |
Asin（ωx+φ） | 0 | 2 | 0 | ﹣2 |
（1）请将上表数据补全，并直接写出函数f（x）的解析式；
（2）当x∈[0， ]时，求函数f（x）的值域．
