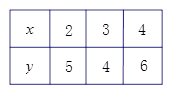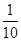题目内容
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
(Ⅰ)求出第4组的频率,并补全频率分布直方图;
(Ⅱ)根据样本频率分布直方图估计样本的中位数;
(Ⅲ)如果用分层抽样的方法从“优秀”和“良好” 的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.(Ⅰ)求出第4组的频率,并补全频率分布直方图;
(Ⅱ)根据样本频率分布直方图估计样本的中位数;
(Ⅲ)如果用分层抽样的方法从“优秀”和“良好” 的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(Ⅰ)0.2,图详见解析;(Ⅱ) ;(Ⅲ)
;(Ⅲ)
 ;(Ⅲ)
;(Ⅲ)
试题分析:在频率分布直方图中需要掌握①:每个小矩形的面积代表落在这个组内数据的频率,所有小矩形的面积和等于1,②利用频率分布直方图可以估计总体的数字特征:众数、中位数、平均数,其中众数是最高矩形的中点横坐标;中位数是两边矩形的面积和各为
 的分界点;平均数等于每个小矩形面积乘以中点横坐标的累加值,③落在每个小矩形内的数据是用其中点横坐标刻画的,(Ⅰ)根据频率和等于1,可计算第四组的频率,然后除以组距,就是这个组的高,即可补全频率分布直方图;(Ⅱ)设样本的中位数为
的分界点;平均数等于每个小矩形面积乘以中点横坐标的累加值,③落在每个小矩形内的数据是用其中点横坐标刻画的,(Ⅰ)根据频率和等于1,可计算第四组的频率,然后除以组距,就是这个组的高,即可补全频率分布直方图;(Ⅱ)设样本的中位数为 ,则
,则 ,可计算
,可计算 的值;(Ⅲ)根据分层抽样可计算出抽取的5人中,优秀3人,良好2人,从中选2人,共有10种结果,其中“全为良好”包括1种结果,∴
的值;(Ⅲ)根据分层抽样可计算出抽取的5人中,优秀3人,良好2人,从中选2人,共有10种结果,其中“全为良好”包括1种结果,∴ .
.
试题解析:(Ⅰ)其它组的频率为(0.01+0.07+0.06+0.02)×5=0.8,
所以第四组的频率为0.2,-----2分
频率/组距是0.04
频率分布图如图: 4分

(Ⅱ)设样本的中位数为
 ,则
,则 5分
5分解得

所以样本中位数的估计值为
 6分
6分(Ⅲ)依题意良好的人数为
 人,优秀的人数为
人,优秀的人数为 人抽取比例为1/8,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人 8分
人抽取比例为1/8,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人 8分法1:记从这5人中选2人至少有1人是优秀为事件M
将考试成绩优秀的三名学生记为A,B,C, 考试成绩良好的两名学生记为a,b
从这5人中任选2人的所有基本事件包括:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,ab
共10个基本事件 9分
事件M含的情况是:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,共9个 10分
所以
 12分
12分法2:P=


练习册系列答案
相关题目

 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数; ,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),┅,第八组[190,195),右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的频数均为4,第六组,第七组,第八组的频率依次构成等差数列。
,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),┅,第八组[190,195),右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的频数均为4,第六组,第七组,第八组的频率依次构成等差数列。
 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 .第二组
.第二组 ; 第八组
; 第八组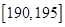 ,下图是按上述分组方法得到的条形图.
,下图是按上述分组方法得到的条形图. 
 以上(含
以上(含 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有 这10个数据的样本平均数为
这10个数据的样本平均数为 ,方差为0.33,则
,方差为0.33,则 ,且祥本容量为140,则中间一组的频数为( )
,且祥本容量为140,则中间一组的频数为( )
 的值如下表所示,如果
的值如下表所示,如果 与
与 线性相关且回归直线方程为
线性相关且回归直线方程为 ,则实数
,则实数 ( )
( )