题目内容
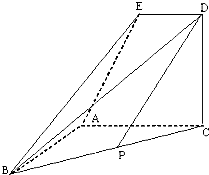
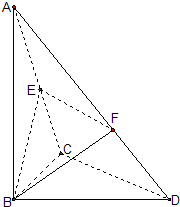
如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,BC=2,CD=
,AB=
,E、F分别为AC、AD上的动点.
(1)若
=
,求证:平面BEF⊥平面ABC;
(2)若
=1,
=2,求平面BEF与平面BCD所成的锐二面角的大小.
| 3 |
| 3 |
(1)若
| AE |
| EC |
| AF |
| FD |
(2)若
| AE |
| EC |
| AF |
| FD |

证明:(1)∵AB⊥平面BCD,
∴AB⊥CD.
又∵CD⊥BC,
∴CD⊥平面ABC.
∵
=
,
∴EF∥CD.
∴EF⊥平面ABC,
∵EF?平面BEF,
∴平面BEF⊥平面ABC.
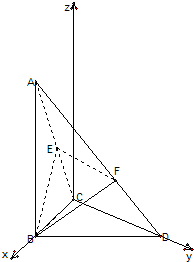
(2)解法一(向量法):
如图建立空间直角坐标系C-xyz
则B(2,0,0),D(0,
,0),A(2,0,
),
∵
=1,
∴E(1,0,
),
∵
=2,
∴F(
,
,
)
∴
=(-1,0,
),
=(-
,
,
),
设
=(x,y,z),
⊥平面BEF,
则
,
设
⊥平面BCD,则
可取(0,0,1),
∴cos<
,
>=
,
所以,平面BEF与平面BCD所成的锐二面角为45°.
方法二(几何法):
延长EF,交CD的延长线于G,连接BG,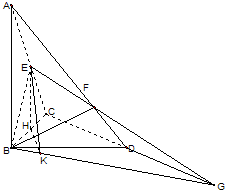
过E作EH⊥BC于H,则EH⊥平面BCD,
过H作HK⊥BG于K,连接EK,则EK⊥BG,
∴∠EKH即为所求二面角的平面角.
∵
=1,
∴AE=
AB=
,
在Rt△BCD中,可以解得HK=
,
∴在Rt△BCD中,∠EKH=45°,即平面BEF与平面BCD所成的锐二面角为45°.
∴AB⊥CD.
又∵CD⊥BC,
∴CD⊥平面ABC.
∵
| AE |
| EC |
| AF |
| FD |
∴EF∥CD.
∴EF⊥平面ABC,
∵EF?平面BEF,
∴平面BEF⊥平面ABC.
(2)解法一(向量法):
如图建立空间直角坐标系C-xyz
则B(2,0,0),D(0,
| 3 |
| 3 |
∵
| AE |
| EC |
∴E(1,0,
| ||
| 2 |
∵
| AF |
| FD |
∴F(
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
∴
| BE |
| ||
| 2 |
| BF |
| 4 |
| 3 |
2
| ||
| 3 |
| ||
| 3 |
设
| n |
| n |
则
|
设
| n1 |
| n1 |
∴cos<
| n |
| n1 |
| ||
| 2 |
所以,平面BEF与平面BCD所成的锐二面角为45°.
方法二(几何法):
延长EF,交CD的延长线于G,连接BG,

过E作EH⊥BC于H,则EH⊥平面BCD,
过H作HK⊥BG于K,连接EK,则EK⊥BG,
∴∠EKH即为所求二面角的平面角.
∵
| AE |
| EC |
∴AE=
| 1 |
| 2 |
| ||
| 2 |
在Rt△BCD中,可以解得HK=
| ||
| 2 |
∴在Rt△BCD中,∠EKH=45°,即平面BEF与平面BCD所成的锐二面角为45°.


练习册系列答案
相关题目