题目内容
1.已知函数f(x)是R上的偶函数,若对于x≥0,都有f(x+2)=-f(x),且当x∈[0,2]时,f(x)=log8(x+1),求f(-2013)+f(2014)的值.分析 根据题意可得;周期为4,可得f(-2013)+f(2014)=f(1)-f(0),即可求解.
解答 解:∵数f(x)是R上的偶函数,
∴f(-x)=f(x),
∵对于x≥0都有f(x+2)=-f(x),
∴f(x+4)=f(x),
∴周期为4,
∵当x∈[0,2)时,f(x)=log8(x+1),
∴f(-2013)+f(2014)=f(1)-f(0)=$\frac{1}{3}$.
点评 本题考查了抽象函数的性质,对数的运算,属于中档题

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
7.不等式组$\left\{\begin{array}{l}{x≥-1}\\{x+y≤3}\\{y≥x+1}\end{array}\right.$表示的平面区域为Ω,直线y=kx-1与区域Ω有公共点,则实数k的取值范围为( )
| A. | (0,3] | B. | [-1,3] | C. | (-∞,-1)∪[3,+∞) | D. | (-∞,1]∪[3,+∞) |
10.下列向量与$\overrightarrow{a}$=(1,2)共线的是( )
| A. | (2,1) | B. | (1,2) | C. | (-1,-2) | D. | (2,-1) |
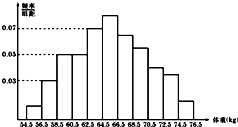 为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.
为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8. 已知函数f(x)=Asin($\frac{π}{3}x$+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$.
已知函数f(x)=Asin($\frac{π}{3}x$+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$.