题目内容
.(12分)已知函数 的定义域为
的定义域为 ,且同时满足:(Ⅰ)对任意
,且同时满足:(Ⅰ)对任意 ,总有
,总有 ;(Ⅱ)
;(Ⅱ)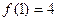 ;(Ⅲ)若
;(Ⅲ)若 ,则有
,则有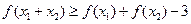
(1)试求 的值;
的值;
(2)试求函数 的最大值;
的最大值;
(3)试证明:当 时,
时, 。
。

(3)当 时,
时,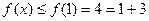
 时,
时,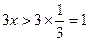
故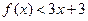
解析

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
题目内容
.(12分)已知函数 的定义域为
的定义域为 ,且同时满足:(Ⅰ)对任意
,且同时满足:(Ⅰ)对任意 ,总有
,总有 ;(Ⅱ)
;(Ⅱ)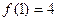 ;(Ⅲ)若
;(Ⅲ)若 ,则有
,则有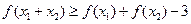
(1)试求 的值;
的值;
(2)试求函数 的最大值;
的最大值;
(3)试证明:当 时,
时, 。
。

(3)当 时,
时,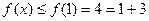
 时,
时,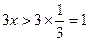
故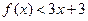
解析

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案